Исследование Vanguard: Рациональная ребалансировка

Исследование Vanguard
Авторы: Yu Zhang (Ph.D.), Harshdeep Ahluwalia, Allison Ying, Michael Rabinovich, Aidan Geysen
Октябрь 2022 г.
Перевод для AssetAllocation.ru

Аналитический подход к решениям по ребалансировке портфеля из нескольких активов и аналитическая информация

Портфели инвесторов должны соответствовать их целям и предпочтениям в отношении рисков, что делает ребалансировку распределения активов в портфеле важной практикой. Являются ли одни методы ребалансировки более эффективными, чем другие, с точки зрения соотношения риска, доходности и затрат?

В этой статье мы представляем новый подход к определению оптимального метода ребалансировки портфеля из нескольких активов путем максимизации капитала портфеля после учета транзакционных издержек. Вместо того чтобы анализировать лишь один исторический период, мы моделируем распределение доходности активов и динамики транзакционных издержек, что жизненно важно при оценке политики ребалансировки. Подход на основе полезности, позволяет определить эффективный с точки зрения риска и доходности метод ребалансировки, одновременно количественно оценивая, насколько он лучше других альтернатив.

Мы считаем, что оптимальные методы предполагают ребалансировку, которая не является ни слишком частой, как ежемесячные или ежеквартальные календарные методы, ни слишком редкой, как восстановление баланса раз в два года. Реализация ежегодной стратегии ребалансировки оптимальна для инвесторов, которые не занимаются сбором налоговых убытков /практика налоговой оптимизации в США – прим. переводчика/ или строгим наблюдением за базовым портфелем, состоящим из пассивных фондов. Большая часть эффективности этих стратегий ребалансировки достигается за счет получения премии за риск по акциям, допуская при этом разумные колебания портфеля.

Вступление

Зачем проводить ребалансировку?

Vanguard считает, что решение о распределении активов, которое учитывает толерантность инвестора к риску, временной горизонт и финансовые цели, является наиболее важным решением в процессе формирования портфеля.

Основная функция ребалансировки портфеля заключается в приведении риска портфеля в соответствие с толерантностью к риску инвестора.

При отсутствии ребалансировки распределение портфеля будет отклоняться от намеченной цели по мере того, как будет меняться доходность его активов, что приведет к гораздо более высокому портфельному риску. Например, портфель с 60% акций и 40% активов с фиксированным доходом на конец 1989 г., если бы он никогда не ребалансировался, к концу 2021 г. имел бы 80% акций, как показано на Рис. 1, что резко отличается от портфеля с ежегодной ребалансировкой.

Рис. 1. Распределение активов в портфеле без ребалансировки в сравнении с ежегодно ребалансируемым портфелем 60/40

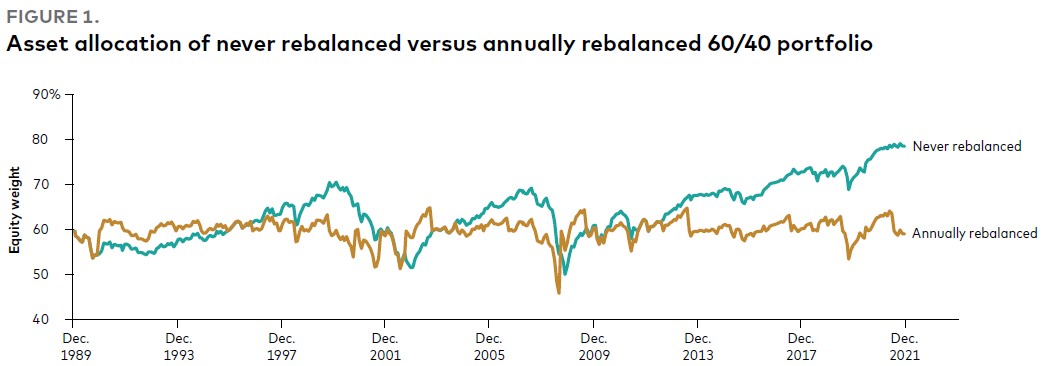
Примечания: Данные о доходности портфеля акций в размере 60% акций/ 40% облигаций относятся к периоду с 31 декабря 1989 г. по 31 декабря 2021 г. На рисунке сравниваются веса акций для портфеля без ребалансировки и портфеля с ребалансировкой в конце каждого года. Доля акций в портфеле 60%/40% может колебаться в пределах от 50% до 80%, если баланс никогда не восстанавливается. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации других стран – Bloomberg Global Aggregate ex-U.S. Index, акции США – Dow Jones Wilshire 5000 с начала 1990 г. по апрель 2005 г. и MSCI US Broad Market Index после, акции за пределами США – MSCI All Country World Index ex USA.

Рис. 2 иллюстрирует дополнительный риск, присущий портфелю 80% акций/20% облигаций, по сравнению с предполагаемым распределением 60% акций/40% облигаций.

Значительные отклонения в периоды повышенной волатильности могут привести к тому, что инвесторы откажутся от своего портфеля из-за несоответствия их толерантности к риску, что приведет к фиксации убытков. С точки зрения поведенческих финансов восстановление баланса играет жизненно важную роль в оказании помощи инвестору для поддержания дисциплины в инвестиционной стратегии и направлено на устранение эмоций при принятии решений во время рыночных потрясений. Это делает ребалансировку важной частью инвестиций.

Когда дело доходит до ребалансировки, существует несколько методов на выбор. Стратегия ребалансировки состоит из решений о частоте, пороге и цели.

• Частота говорит о том, как часто следует контролировать распределение портфеля. Частота мониторинга может быть ежедневной, еженедельной, ежемесячной, ежеквартальной, полугодовой, ежегодной и т.д.
• Порог определяет, насколько допустимо отклонение распределения активов от целевого показателя. Например, порог в 1%, или 2% и т.д.
• Наконец, Цель сообщает, насколько далеко от цели будет восстановлен баланс портфеля; можно выбрать между полным возвратом к целевому распределению, половиной пути между целью и порогом или возвратом к краю порога.

Рис. 2. Сочетание активов определяет спектр риска

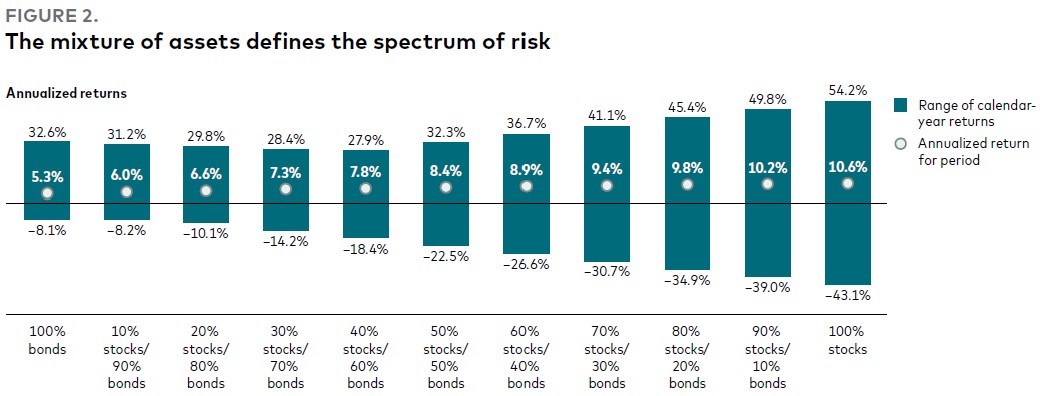
Распределения активов от 100% облигаций до 100% акций с шагом 10%
Годовые доходности:

• Диапазон доходностей за календарный год
• Среднегодовая доходность за период

Примечания: Данные о доходностях относятся к периоду с 1 января 1926 г. по 31 декабря 2021 г. На рисунке показана максимальная и минимальная годовая доходность для данного распределения активов портфеля за данный период времени. Ребалансировка портфелей проводилась ежемесячно. Результаты отображаются на основе данных до вычета налогов. Облигации США представлены Standard & Poor’s High Grade Corporate Index с 1926 по 1968 гг.; Citigroup High Grade Index с 1969 по 1972 гг.; Lehman Brothers U.S. Long Credit AA Index с 1973 по 1975 гг.; Barclays U.S. Aggregate Bond Index с 1976 по 2009 гг., и Spliced Barclays U.S. Aggregate Float Adjusted Bond Index после. Акции США представлены Standard & Poor’s 90 с 1926 по 1957 гг.; Standard & Poor’s 500 с 1957 по 1974 гг.; Wilshire 5000 с 1976 по 1977 гг., Wilshire 5000 Index с 1975 до 2005 гг.; MSCI US Broad Market Index до 2013 г. и индексом CRSP US Total Market Index после.

Инвесторы, консультанты и управляющие активами используют три популярных метода ребалансировки портфелей, которые включают выбор частоты, порога и цели. На Рис. 3 описаны методы ребалансировки, которые анализируются в данной статье.

1. Ребалансировка на основе календаря: Подход к ребалансировке на основе календаря определяет периодичность ребалансировки активов портфеля обратно к целевому распределению активов. Более частые календарные методы ребалансировки приводят к снижению ошибки слежения и более высоким транзакционным издержкам при отсутствии денежных потоков, способствующих ребалансировке.
2. Ребалансировка на основе порога: Этот метод позволяет распределению портфеля смещаться в пределах допустимого порога, при этом ребалансировка запускается только при нарушении порога. Одним из основных недостатков ребалансировки на основе порога является то, что она требует ежедневного мониторинга портфеля и, таким образом, непрактична для инвесторов, которые управляют своими портфелями самостоятельно. Чем ниже порог, тем меньше ошибка слежения и тем выше стоимость транзакционных издержек.
3. Ребалансировка на основе календаря и порога: этот метод сочетает в себе подходы к ребалансировке на основе календаря и порога. В соответствии с календарной периодичностью отслеживаются веса распределения активов, однако торговые операции осуществляются лишь в том случае, если вес активов в портфеле превышает порог ребалансировки.

Рис. 3. Распространенные методы ребалансировки и их характеристики

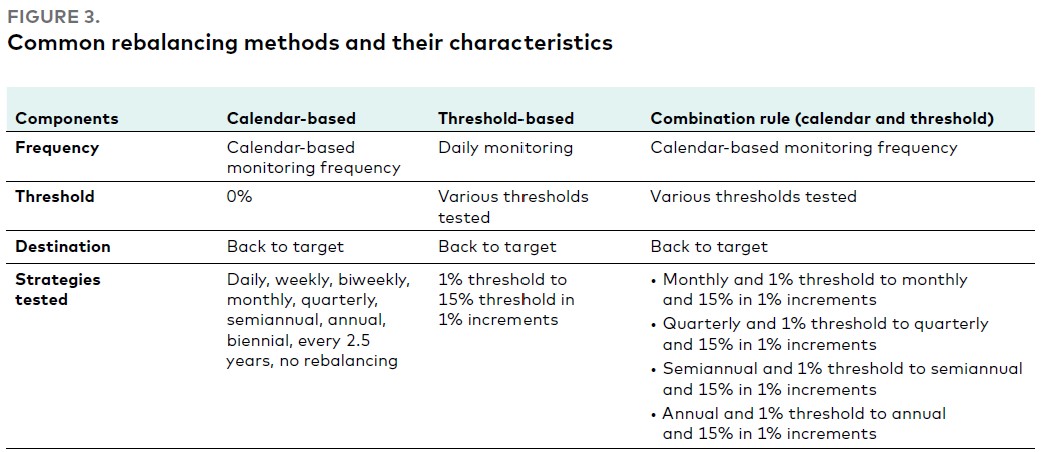
На основе календаря:

• Частота: мониторинг на основе календаря
• Порог: 0%
• Цель: возврат к цели
• Протестированные стратегии: ежедневно, еженедельно, раз в две недели, ежемесячно, ежеквартально, раз в полгода, ежегодно, раз в 2 года, раз в 2,5 года, без ребалансировки

На основе порога:

• Частота: ежедневный мониторинг
• Порог: протестированы различные пороговые значения
• Цель: возврат к цели
• Протестированные стратегии: порог от 1% до 15% с шагом в 1%

Комбинированное правило (на основе календаря и порога):

• Частота: мониторинг на основе календаря
• Порог: протестированы различные пороговые значения
• Цель: возврат к цели
• Протестированные стратегии: • Ежемесячно с порогом от 1% до 15% с шагом 1%, • Ежеквартально с порогом от 1% до 15% с шагом 1%, • Раз в полгода с порогом от 1% до 15% с шагом 1%, • Ежегодно с порогом от 1% до 15% с шагом 1%

С учетом многочисленных стратегий ребалансировки, которые могут быть реализованы, являются ли одни стратегии более эффективными с точки зрения риска и доходности, чем другие?

В этой статье мы представляем новый подход к определению оптимальной стратегии ребалансировки портфеля с несколькими активами. Вместо того чтобы анализировать лишь один исторический период, мы моделируем распределение доходности активов (аналогично Vanguard Capital Markets Model или VCMM), которое охватывает множество периодов, и динамическое распределение транзакционных издержек, отражающее важную особенность этих издержек – то, что они увеличиваются с ростом волатильности рынка, что является жизненно важным фактором при выборе политики ребалансировки. Подход к оптимизации на основе полезности позволяет определить эффективный с точки зрения риска и прибыли метод ребалансировки, а также количественно оценить, насколько он лучше других вариантов ребалансировки.

Эта статья состоит из четырех частей. В первом разделе мы приводим краткий обзор литературы. Во втором разделе мы предлагаем обзор нашей модели прогнозирования доходности и транзакционных издержек. В третьем разделе мы описываем систему принятия решений на основе полезности. В четвертом разделе, мы выделяем важные выводы, полученные с помощью количественного подхода и аналитики.

Улучшение анализа, лежащего в основе решений о ребалансировке

В литературе существует огромное разнообразие исследований, посвященных ребалансировке. В целом, исследования правильно подчеркивают важность ребалансировки портфеля. Однако более глубокие идеи и выводы о ребалансировке довольно сильно различаются и могут быть классифицированы как:

• Исследования, в которых делается вывод об отсутствии оптимального метода, такие как Zilbering et al. (2015) и Czasonis, Pradhan и Turkington (2020).
• Исследования, в которых рекомендуется оптимальный метод ребалансировки, основанный на доходностях одного конкретного периода, такие как Harjoto и Jones (2006), De Juan et al. (2018) и Plaxco and Arnott (2002).
• Исследования, в которых рекомендуется оптимальный метод ребалансировки, основанный на доходностях на основе моделирования, но со статическими транзакционными издержками, такие как Buetow et al. (2002), Masters (2003), Donohue and Yip (2003), Sun et al. (2006) и Kritzman, Myrgren и Page (2009).
• Исследования, в которых рекомендуется оптимальный метод ребалансировки, основанный на доходностях на основе моделирования и динамических транзакционных издержках, такие как Jones and Stine (2010), Chan and Ramkumar (2011) и Norges Bank Investment Management (2012). Наше исследование относится к этой категории.

Ниже приведены несколько недостатков первых трех подходов:

1. Отсутствие оптимального метода: Когда нет системы принятия решений или анализа, зависящего от исторического периода, а иногда нет и конкретной рекомендации. Мы считаем, что этот подход не позволяет выявить неэффективные методы ребалансировки и не является идеальным.
2. Анализ, зависящий от одного конкретного периода: История предоставляет очень мало примеров для оценки ребалансировки. Привязка выводов только к одной траектории доходности, всего с несколькими изменчивыми событиями, может привести к ошибочным выводам. Вместо этого анализ должен учитывать неопределенность будущих доходностей, что делает важным вкладом предположения о распределении рынков капитала. В этой статье мы используем сокращенную версию VCMM для создания распределения ежедневной доходности активов, поскольку методы, основанные на пороговых значениях, требуют ежедневного моделирования доходности. Важные особенности этой вероятностной модели освещены в следующем разделе.
3. Игнорирование или допущение статичности транзакционных издержек: Большинство исследований опускают транзакционные издержки или предполагают, что транзакционные издержки статичны. Ни то, ни другое не является разумным подходом, особенно для портфеля из ETFs или отдельных ценных бумаг, стоимость которых, вероятно, будет включать спреды между спросом и предложением и брокерские комиссии (для взаимных фондов транзакционные издержки неявно оплачиваются всеми инвесторами в связи с покупкой или продажей ценных бумаг внутри фонда). Во-первых, мы обнаруживаем, что транзакционные издержки не являются статичными с течением времени, а чувствительны к волатильности рынка и могут увеличиваться в десятки раз в периоды рыночных потрясений. Таким образом, при анализе ребалансировки важно учитывать динамические транзакционные издержки. Вместо того чтобы предполагать статические транзакционные издержки, мы моделируем издержки как функцию волатильности рынка, что является важным прогностическим фактором. Во-вторых, мы прогнозируем колоколообразную кривую транзакционных издержек, как и доходность активов.

ВАЖНО: Прогнозы и другая информация, генерируемая VCMM относительно вероятности различных результатов инвестирования, носят гипотетический характер, не отражают фактические результаты инвестиций и не являются гарантиями будущих результатов. Распределение результатов доходностей от VCMM получено из 10’000 симуляций для каждого смоделированного класса активов. Моделирование по состоянию на июнь 2022 г. Результаты работы модели могут отличаться при каждом использовании и с течением времени.

Аналитический подход, основанный на моделировании, может дать более глубокое понимание, чем исторический анализ, основанный на единственной траектории. Как обсуждается далее в статье, вероятностный подход дает более глубокое представление о том, насколько хорошо подходы к ребалансировке работают в различных средах, и количественно определяет соотношение выгод от ребалансировки между транзакционными издержками и рыночными факторами.

Механизм прогнозирования

В этой статье мы используем вероятностный подход к прогнозированию доходности активов и транзакционных издержек. При этом мы используем результаты более чем десятилетних исследований Vanguard, по сравнению с патентованным VCMM, для прогнозирования доходности, волатильности и корреляций. Ниже описаны ключевые особенности модели прогнозирования доходности активов, которую мы использовали:

1. Структура распределения: Прогнозирование диапазона возможных доходностей активов, волатильности и корреляций позволяет более глубоко оценить соотношение риска и доходности по сравнению с прогнозированием одного значения. Это позволяет инвесторам принимать объективные решения о восстановлении баланса.
2. Распределения, отличающиеся от нормального: Хорошо известно, что доходность активов не подчиняется нормальному распределению, причем хвостовые доходности более вероятны, чем предполагается при нормальном распределении. Эта полезная характеристика отражена в наших симуляциях.
3. Прогнозирование фундаментальных факторов: В качестве первого шага модель прогнозирует факторы доходности активов, такие как процентные ставки, инфляция, экономический рост, соотношение цена/прибыль (P/E) акций и волатильность рынка. Эти прогнозы динамичны, поскольку эволюция одного фундаментального фактора влияет на другой.
4. Прогнозы доходности на основе фундаментальных показателей: На втором шаге доходности активов и операционные издержки моделируются как функции фундаментальных факторов, описанных выше. Например, доходность акций – это сумма дивидендной доходности, процентного изменения соотношения P/E и роста прибыли, которые могут быть выражены в терминах прогнозов соотношения P/E.
5. Кластеризация волатильности: Модель включает в себя функцию кластеризации волатильности акций, поскольку периоды высокой волатильности акций, как правило, группируются вместе. Эта жизненно важная функция встроена с использованием модели GARCH (generalized autoregressive conditional heteroskedasticity – обобщенная авторегрессионная условная гетероскедастичность).
6. Совместное прогнозирование: Модель совместно прогнозирует доходность активов и транзакционные издержки с помощью метода Монте-Карло на основе регрессии, тем самым сохраняя любую взаимную корреляцию между ними.
7. Транзакционные издержки: Транзакционные издержки моделируются как функция спредов спроса и предложения, которые чувствительны к волатильности рынка. Во времена рыночных потрясений спреды спроса и предложения резко возрастают, как показано на Рис. 4. Вместо того, чтобы предполагать статичные спреды спроса и предложения и транзакционные издержки, мы моделируем их и другие макроэкономические переменные как чувствительные к волатильности рынка. Это приводит к скорректированному показателю R² более 87%. (R² – показатель того, в какой степени изменчивость транзакционных издержек может быть объяснена вышеупомянутыми независимыми переменными.)

Для получения подробного обзора VCMM обратитесь к Davis et al. (2014) и Davis et al. (2022).

Рис. 4. Транзакционные издержки чувствительны к волатильности рынка

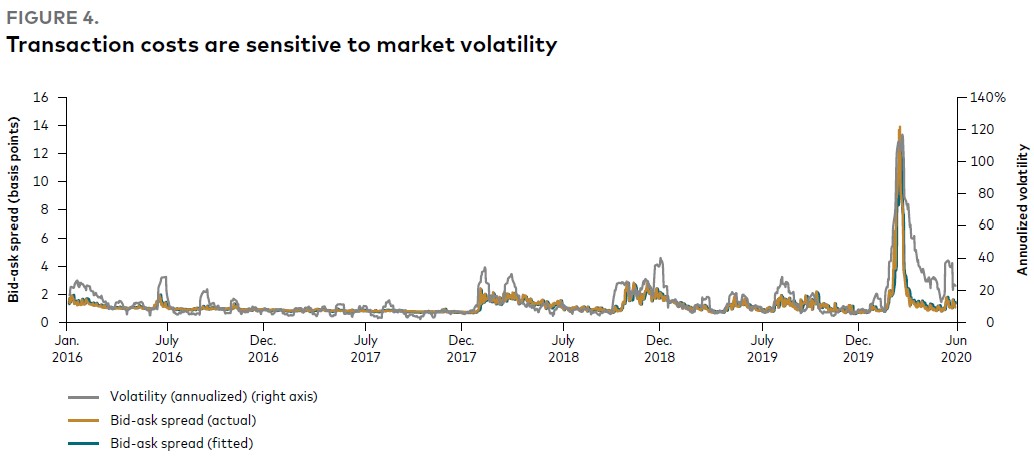
– Волатильность (в годовом исчислении) (правая шкала)
– Спред между спросом и предложением (фактический)
– Спред между спросом и предложением (скорректированный)

Примечания: Данные о спредах между спросом и предложением приведены с 1 января 2016 г. по 30 июня 2020 г. На рисунке показан фактический и скорректированный или прогнозируемый спрэд спроса и предложения на временном интервале. Волатильность – это 10-дневная волатильность дневной доходности, основанная на цене закрытия индекса Standard & Poor’s 500. Базисный пункт – одна сотая процентного пункта.

Система принятия решений

При сравнении методов ребалансировки качественная оценка требует суждения о компромиссах, что может быть затруднительно, когда активы с более высокой доходностью характеризуются более высокой волатильностью. Другими словами, если одно правило ребалансировки обеспечивает более высокую доходность, пусть и с большей волатильностью, следует ли отдавать ему предпочтение? Одним из преимуществ подхода на основе полезности является то, что он позволяет нам объективно сравнивать полезность по различным правилам ребалансировки, а не путем неубедительных сравнений риска и прибыли.

Аналогично модели Vanguard Asset Allocation Model (VAAM) (Aliaga et al., 2019), мы внедряем систему оптимизации на основе полезности, чтобы помочь оценить различные стратегии ребалансировки и определить оптимальную стратегию. Наша система выбирает стратегию ребалансировки, которая максимизирует ожидаемую полезность капитала инвестора после учета транзакционных издержек в конце данного инвестиционного периода (к примеру, 10 лет).

Таким образом, для данного распределения активов оптимальной стратегией является стратегия ребалансировки, имеющая наивысший показатель полезности.
.
Обзор программы проиллюстрирован на Рис. 5, в то время как технические детали функции полезности обсуждаются в Приложении А-1. В дополнение к оптимальному выбору вычисляется несколько интересных аналитических показателей портфеля, таких как распределение доходности, волатильность, коэффициент Шарпа, транзакционные издержки, ошибка слежения, количество событий ребалансировки, размер события и оборачиваемость.

Структура оптимизации требует следующих входных данных: 1) распределение доходности активов, 2) распределение транзакционных издержек, 3) неприятие инвестором риска и 4) ограничения (опционально). Платформа оптимизации на основе полезности также позволяет при необходимости встраивать ограничения. Например, ограничения на максимальные ожидаемые затраты на транзакцию или максимально допустимую ошибку отслеживания могут быть легко реализованы в рамках этой структуры.

Рис. 5. Процесс оптимизации для оценки стратегий ребалансировки

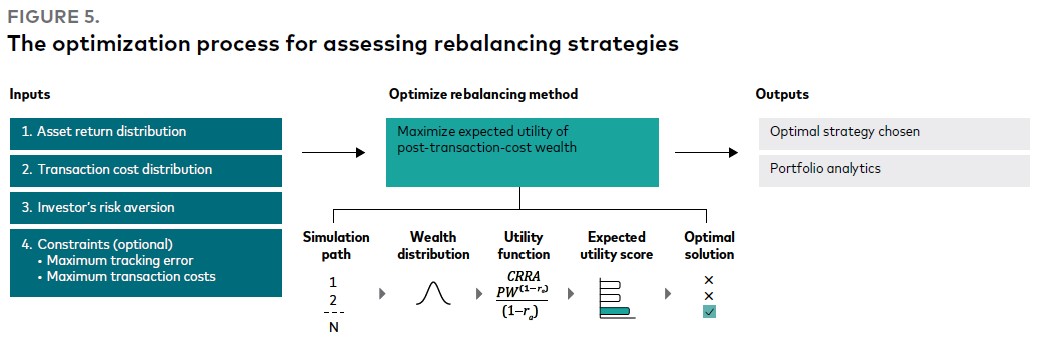
На входе:

1. Распределение доходностей активов
2. Распределение стоимости трнзакций
3. Неприятие риска инвестором
4. Ограничения (опционально):
   • Максимальная ошибка слежения
   • Максимальные транзакционные издержки

Метод оптимизации ребалансировки:
(максимизация ожидаемой полезности богатства с учетом транзакционных издержек)

• Путь моделирования
• Распределение богатства
• Функция полезности
• Ожидаемый показатель полезности
• Оптимальное решение

На выходе:

• Оптимальная выбранная стратегия
• Портфельная аналитика

Идеи

С использованием нашей новой структуры мы определяем, какая стратегия ребалансировки является наиболее эффективной с точки зрения риска, доходности и затрат. При этом мы также можем количественно оценить, насколько одна стратегия лучше другой. Кроме того, мы анализируем, какая часть выгоды достигается за счет снижения транзакционных издержек, в сравнении с тем, какая часть определяется рынком. Наконец, мы обсудим, получают ли оптимальные методы ребалансировки наибольшее преимущество в условиях высокой волатильности рынка или в нормальных условиях.

Прежде чем обсуждать наши выводы, мы кратко обсудим несколько соображений, которые мы не учитывали при изучении того, как эти факторы повлияют на результаты.

• Денежные потоки: Управление денежными потоками от периодических взносов в активы, имеющие недостаточный вес – отличный способ естественным и эффективным образом сбалансировать портфель. Аналогичным образом для ребалансировки может быть использовано изъятие средств из портфелей. Следовательно, учет денежных потоков при анализе привел бы к еще более редкой ребалансировке или более широким пороговым значениям, чем оптимальные.
• Сбор налоговых убытков: Для инвесторов, участвующих в сборе налоговых убытков, можно ожидать более частого мониторинга портфеля. Получение налоговых убытков может уменьшить ваши налоговые обязательства. Ожидается, что это преимущество компенсирует несколько более высокие транзакционные издержки, связанные с частой ребалансировкой. Таким образом, наши выводы могут быть неприменимы при сборе налоговых убытков, когда решения о ребалансировке являются более персонализированными.
• Налоги: Ребалансировка портфеля обычно приводит к продаже активов, стоимость которых выросла; этот рост стоимости приводит к увеличению избыточного веса при их распределении, тем самым вызывая событие ребалансировки. Во время таких событий прирост капитала будет облагаться налогом, если активы хранятся на налогооблагаемых счетах. Вообще говоря, мы ожидаем, что аналогичная или даже менее частая стратегия ребалансировки будет оптимальной, поскольку учет налогов приведет к более высокому налоговому бремени, тем самым увеличивая стоимость ребалансировки.

Ребалансировка на основе календаря

Методы на основе календаря просты и легки в реализации. Среди правил ребалансировки на основе календаря мы находим, что ежегодная ребалансировка портфеля является оптимальной для различных распределений между акциями и облигациями. Например, ежегодная ребалансировка имеет самые высокие показатели по шкале оптимальности для портфеля из 60% акций/40% облигаций, как показано на Рис. 6, по сравнению с другими методами, основанными на календаре.

В целом, слишком частое или редкое восстановление баланса не является эффективным с точки зрения риска, доходности и затрат, о чем свидетельствует форма горба на Рис. 6. Стратегии слишком частого восстановления баланса требуют более высоких затрат и операционных издержек и имеют более серьезные налоговые последствия в рамках налогооблагаемых счетов. В действительности наша система определяет ежедневную ребалансировку на основе календаря как наиболее неэффективную.

С другой стороны, слишком редкая ребалансировка, такая как раз в 2,5 года или вообще отсутствие ребалансировки, приводят к тому, что портфель со временем слишком сильно отклоняется от целевого распределения, что приводит к несоответствию толерантности инвестора к риску.

Система принятия решений на основе полезности предотвращает это несоответствие. Ежегодное изменение баланса является оптимальным с точки зрения соотношения затрат и выгод, оставаясь при этом в соответствии с предпочтениями инвестора в отношении риска.

Преимущество одного правила ребалансировки перед другим может быть количественно оценено в терминах эквивалента платы за определенность (ЭПО), который является шкалой оптимальности на Рис. 6. ЭПО – это плата, которая оставила бы инвестора равнодушной, если бы ему был предоставлен выбор между оптимальным решением с оплатой и неоптимальным решением без какой-либо оплаты. Другими словами, это преимущество оптимальной стратегии. Например, мы обнаруживаем, что ЭПО ежегодной ребалансировки составляет 51 базисный пункт (0,51%) по сравнению с ежедневным восстановлением баланса.

Рис. 6. Методы ребалансировки на основе календаря

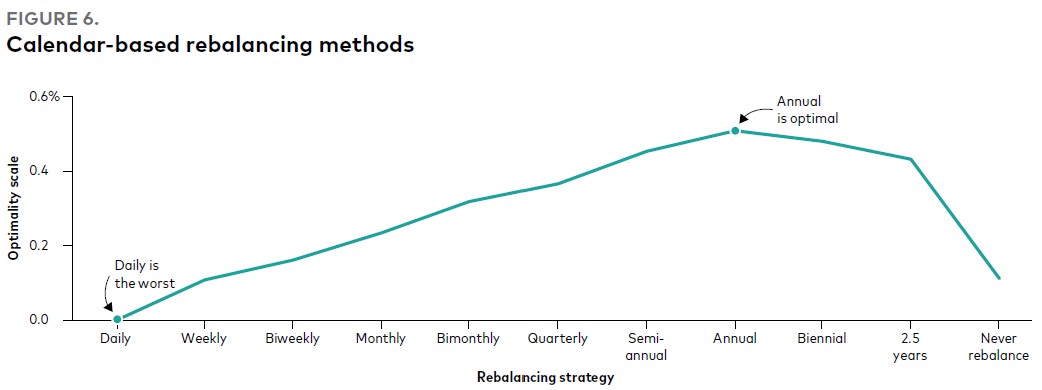
Стратегия ребалансировки:
Ежедневно (худший вариант) / еженедельно / раз в две недели / ежемесячно / ежеквартально / раз в полгода / ежегодно (оптимальный вариант) / раз в два года / раз в 2,5 года / без ребалансировки

Примечания: Результаты основаны на моделировании с помощью нашего механизма прогнозирования и максимизации стоимости активов после учета транзакционных издержек для портфеля 60/40 при различных стратегиях ребалансировки, показанных выше. Индекс оптимальности – это «эквивалент платы за определенность», или выгода от выбора оптимальной стратегии ребалансировки относительно ежедневной ребалансировки, либо, наоборот, комиссия, которую инвестор был бы готов заплатить относительно ежедневной ребалансировки. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Ребалансировка на основе порога

Ребалансировка на основе пороговых значений иногда используется управляющими активами фондов со многими активами, где целью является поддержание низкой ошибки слежения. Например, если желательна ожидаемая ошибка слежения менее или равна 20 базисным пунктам, то для портфеля 60/40 оптимальной является ребалансировка на основе порога 3%

Ребалансировка на основе календаря и порога

На Рис. 7 показано, что в соответствии с правилами на основе календаря и порога менее частая ребалансировка, например, ежегодно с порогом 1%, является наиболее эффективной. Обратите внимание, что нет существенной разницы в использовании порога 1% или 2% при годовой периодичности. Мы заметили, что ежемесячная ребалансировка с порогом менее эффективна, но все же лучше, чем полное отсутствие ребалансировки. Менее частые календарные и пороговые методы также относительно просты в применении инвесторами.

Рис. 7. Ребалансировка на основе календаря и порога без ограничений

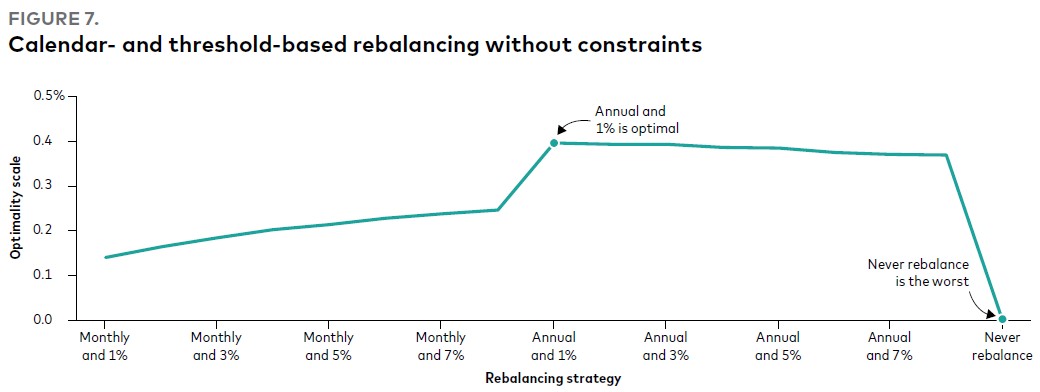
Стратегия ребалансировки:
Ежемесячно и 1% / Ежемесячно и 3% / Ежемесячно и 5% / Ежемесячно и 7% / Ежегодно и 1% (оптимальный вариант) / Ежегодно и 3% / Ежегодно и 5% / Ежегодно и 7% / Без ребалансировки (худший вариант)

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования и максимизации стоимости активов после учета транзакционных издержек для портфеля 60/40 при различных стратегиях ребалансировки, показанных выше. Индекс оптимальности – это «эквивалент платы за определенность», или выгода от выбора оптимальной стратегии ребалансировки относительно отсутствия ребалансировки, либо, наоборот, комиссия, которую инвестор был бы готов заплатить за то, чтобы никогда не восстанавливать баланс. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Ребалансировка в случае ограничений

В некоторых случаях для достижения определенных инвестиционных целей требуется решение по ребалансировке с учетом ограничений, например, с максимальной ожидаемой ошибкой слежения.

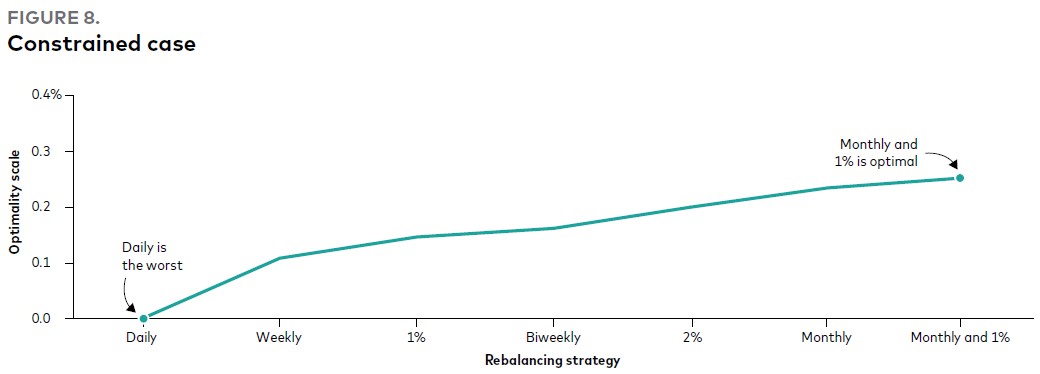
Например, на Рис. 8 показано, что среди всех стратегий ребалансировки с ожидаемой ошибкой слежения менее 15 базисных пунктов оптимальной является «ежемесячно и 1%». Обратите внимание, что нет существенной разницы между ребалансировкой «ежемесячно и 1%», «ежемесячно» и «2%». Наша структура достаточно гибка, чтобы учитывать другие типы ограничений.

Рис. 8. Случай с учетом ограничений

Стратегия ребалансировки:
Ежедневно (худший вариант) / Еженедельно / 1% / Раза в две недели / 2% / Ежемесячно / Ежемесячно и 1% (оптимальный вариант)

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования и максимизации стоимости активов после учета транзакционных издержек для портфеля 60/40 при различных стратегиях ребалансировки, показанных выше. Шкала оптимальности – «эквивалент платы за определенность», или выгода от выбора оптимальной стратегии ребалансировки относительно ежедневной ребалансировки или, наоборот, комиссии, которую инвестор был бы готов заплатить относительно ежедневной ребалансировки. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

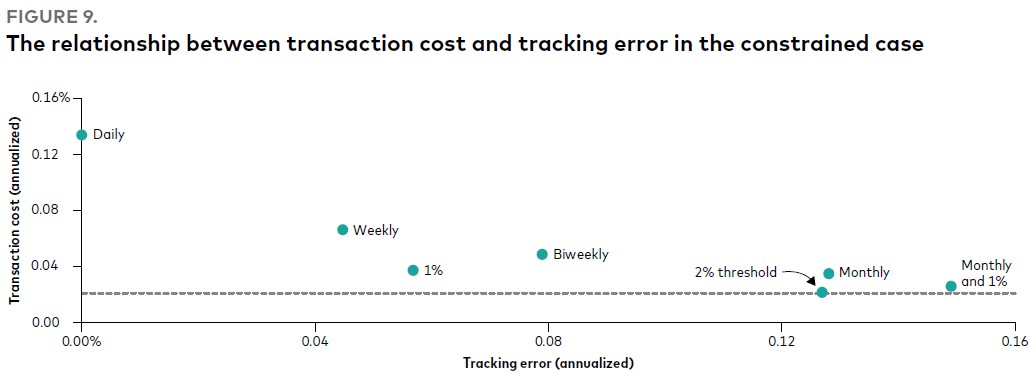
На Рис. 9 показана взаимосвязь между ошибкой слежения и стоимостью транзакции в сценарии с ограничениями. Ожидается, что при ребалансировке на основе порога 2% транзакционные издержки будут ниже, чем при ежемесячной стратегии, а также при стратегии ребалансировки «ежемесячно и 1%».

Рис. 9. Взаимосвязь между транзакционными издержками и ошибкой слежения в случае ограничений

х: Ошибка слежения (% годовых),   y: Транзакционные издержки (% годовых)

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования для портфеля 60/40. Точки «Ежедневно», «Еженедельно», «Раз в две недели» и «Ежемесячно» относятся к частоте ребалансировки на основе календаря; проценты – к пороговой ребалансировке, «ежемесячно и 1%» – на основе календаря и порога. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США –MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Какой метод в целом является оптимальным?

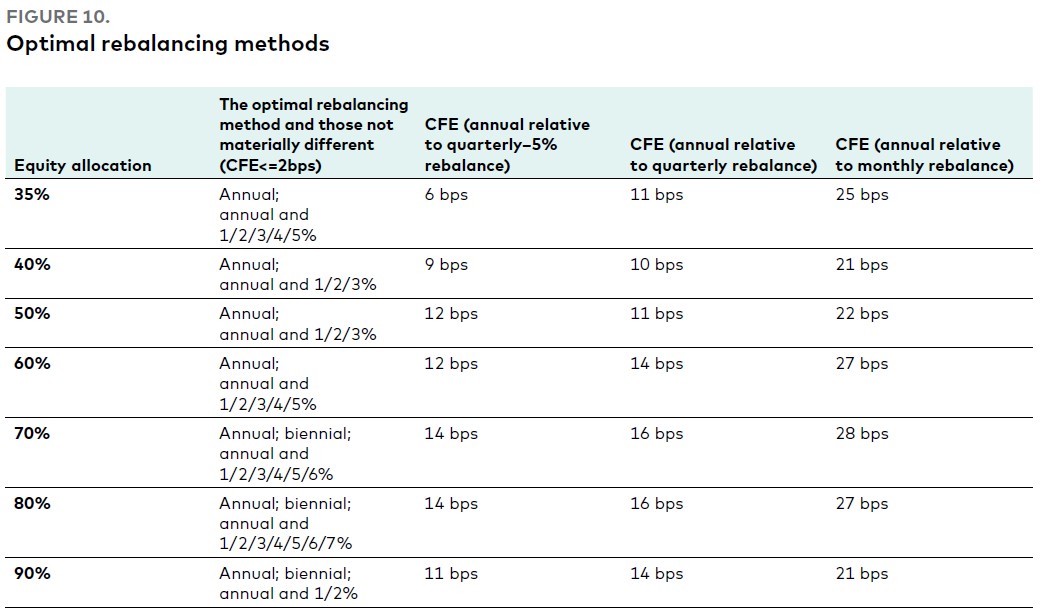
Какой метод ребалансировки является оптимальным среди различных вариантов на основе календаря, порога и календаря-и-порога? Согласуется ли оптимальный выбор с различными вариантами распределения активов? На Рис. 10 показано, что ежегодная ребалансировка (или ежегодная ребалансировка с порогом 1% или 2%) является оптимальной стратегией для различных протестированных распределений активов. С точки зрения простоты внедрения ежегодная ребалансировка является разумной рекомендацией. Это также приводит к снижению транзакционных издержек и соответствует толерантности инвестора к риску.

Мы также сравнили оптимальную стратегию ребалансировки с популярными стратегиями ребалансировки, такими как «ежеквартально и 5%», «ежеквартально» и «ежемесячно». Ежегодная ребалансировка превосходит популярные стратегии, когда дело доходит до статистической значимости. Её выгода по сравнению с ребалансировкой «ежеквартально и 5%» составляет от 6 до 14 базисных пунктов, по сравнению с ежеквартальной ребалансировкой (без порогового значения) – от 10 до 16 базисных пунктов, по сравнению с ежемесячной ребалансировкой (без порогового значения) – от 21 до 28 базисных пунктов.

Подводя итог, наша рекомендация для большинства инвесторов – тех, кто не участвует в сборе налоговых убытков или не требует минимальной ошибки слежения эталонного портфеля – заключается в следовании методу ежегодной ребалансировки.

Рис. 10. Оптимальные методы ребалансировки

Столбцы:

• Доля акций
• Оптимальный метод ребалансировки и те, что слабо отличаются (ЭПО менее 2 бп)
• ЭПО ребалансировки «ежегодно» по отношению к «ежеквартально и 5%»
• ЭПО ребалансировки «ежегодно» по отношению к «ежеквартально
• ЭПО ребалансировки «ежегодно» по отношению к «ежемесячно»

Строки:

• 35% акций – Ежегодно, ежегодно и 1/2/3/4/5% – 6 бп / 11 бп / 25 бп
• 40% акций – Ежегодно, ежегодно и 1/2/3% – 9 бп. / 10 бп / 21 бп
• 50% акций – Ежегодно, ежегодно и 1/2/3% – 12 бп / 11 бп / 22 бп
• 60% акций – Ежегодно, ежегодно и 1/2/3/4/5% –12 бп / 14 бп / 27 бп
• 70% акций – Ежегодно, раз в 2 года, ежегодно и 1/2/3/4/5/6% – 14 бп / 16 бп / 28 бп
• 80% акций – Ежегодно, раз в 2 года, ежегодно и 1/2/3/4/5/6/7% – 14 бп / 16 бп / 27 бп
• 90% акций – Ежегодно, раз в 2 года, ежегодно и 1/2% – 11 бп / 14 бп / 21 бп

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования и максимизации стоимости активов после транзакции для различных портфелей и стратегий ребалансировки, показанных выше. ЭПО – «эквивалент платы за определенность» – преимущество выбора оптимальной стратегии ребалансировки по сравнению с другим методом ребалансировки или наоборот, плата, которую инвестор был бы готов заплатить по сравнению с другим методом ребалансировки. «бп» – базисные пункты. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Преимущество менее частой ребалансировки

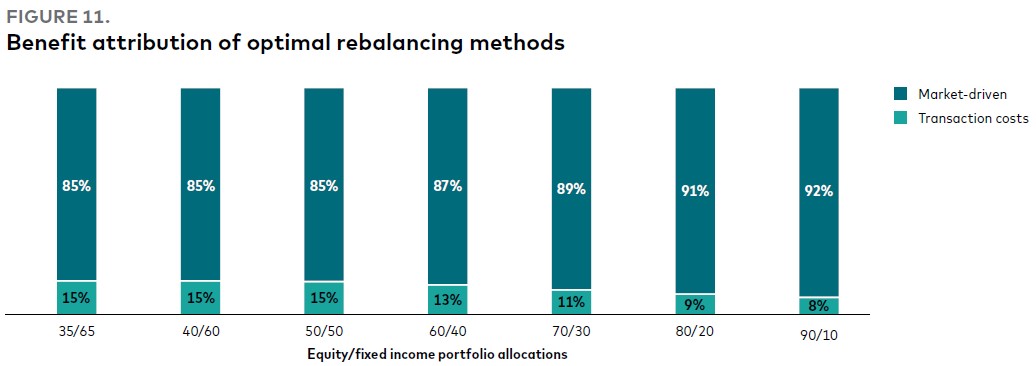
Насколько выгодна ежегодная ребалансировка за счет снижения транзакционных издержек по сравнению с более частой календарной моделью, такой как ежемесячная ребалансировка? На Рис. 11 показано, что 10-20% выгоды можно отнести на счет снижения транзакционных издержек. Оставшиеся 80-90% можно отнести на счет рыночных причин, таких как получение премии за риск акций за счет менее частой ребалансировки. Как отмечалось ранее, ежегодная ребалансировка является оптимальной даже с учетом возможного смещения распределения, поскольку наша система гарантирует, что это будет в соответствии с толерантностью инвестора к риску.

Рис. 11. Определение преимуществ оптимальных методов ребалансировки

Распределение Акции/Инструменты с фиксированным доходом в портфеле

• Выгода от движений рынка
• Транзакционные издержки

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования и максимизации стоимости капитала с учетом транзакционных издержек для различных портфелей и стратегий ребалансировки, показанных выше. Анализ показывает, какая часть ожидаемой выгоды возникает в результате снижения транзакционных издержек по сравнению с выгодой от движений рынка между ежегодной ребалансировкой и ежемесячной ребалансировкой. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Ребалансировка в условиях волатильности

Следует ли ребалансировать портфель в периоды высокой волатильности фондового рынка? То есть следует ли продавать инструменты с фиксированным доходом, а вырученные средства использовать для покупки акций? Чтобы ответить на этот вопрос, мы сгруппировали результаты моделирования по квинтилям волатильности фондового рынка и оценили, является ли ежегодная ребалансировка более эффективной, чем ежемесячная.

Рис. 12 показывает ЭПО (эквивалент платы за определенность) годовой ребалансировки по отношению к ежемесячной ребалансировке в разбивке на пять квинтилей на основе волатильности. Мы считаем, что менее частое восстановление баланса эффективно в периоды рыночных потрясений, о чем свидетельствует высокий ЭПО 1,52% (указан на шкале оптимальности) для ежегодной стратегии ребалансировки. Хотя кому-то может повезти, если время от времени проводить ежемесячную ребалансировку, когда фондовые рынки восстанавливаются сразу же после события ребалансировки, наш анализ показывает, что в среднем часто ребалансировать неэффективно, особенно в периоды высокой волатильности. Как мы проиллюстрировали на Рис. 4, транзакционные издержки растут в нестабильных условиях, что делает восстановление баланса дорогостоящим мероприятием.

Другая причина состоит в том, что можно провести ребалансировку в одном направлении, а затем придется совершить обратную транзакцию, поскольку рынок стал двигаться в обратном направлении, что может происходить в такие периоды потрясений. Использование вместо этого менее частой стратегии ребалансировки довольно эффективно, поскольку позволяет избежать высоких транзакционных издержек и ненужных сделок.

Рис. 12. Преимущества более редкой ребалансировки во время волатильности рынков

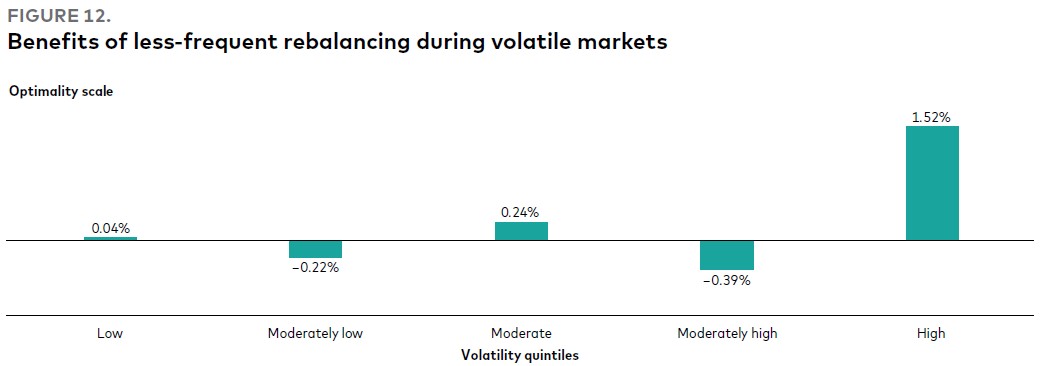
Квинтили волатильности:

• Низкая волатильность: ЭПО +0,04%
• Умеренно низкая волатильность: ЭПО -0,22%
• Умеренная волатильность: ЭПО +0,24%
• Умеренно высокая волатильность: ЭПО -0,39%
• Высокая волатильность: ЭПО +1,52%

Примечания: Результаты основаны на моделировании с помощью механизма прогнозирования и максимизации стоимости активов после учета транзакционных издержек для портфеля 60/40 путем группировки результатов моделирования в соответствии с волатильностью доходности портфеля. Облигации США представлены Bloomberg U.S. Aggregate Bond Index, облигации за пределами США – Bloomberg Global Aggregate ex-U.S. Index, акции США – MSCI US Broad Market Index и акции за пределами США – MSCI All Country World Index ex USA. Данные приведены по состоянию на июнь 2022 г.

Выводы

Мы предлагаем структуру для определения эффективной с точки зрения риска и прибыли стратегии ребалансировки путем максимизации ожидаемой полезности капитала после учета транзакционных издержек. Система требует прогнозирования распределения доходности активов и транзакционных издержек, которые являются критическими факторами при оценке ребалансировки.

Мы считаем, что оптимальные методы ребалансировки не являются ни слишком частыми, как ежемесячные или ежеквартальные методы на основе календаря, ни слишком редкими, как ребалансировка лишь раз в два года. Проведение ежегодной ребалансировки оптимально для инвесторов, которые не участвуют в сборе налоговых убытков, и для кого не требуется строгое отслеживание эталонного портфеля с несколькими активами.

Большая часть эффективности оптимальных стратегий ребалансировки обусловлена рыночными причинами, такими как получение премии за риск акций. Наш анализ моделирует транзакционные издержки ETFs и может быть непосредственно применен к портфелям, основанным на ETFs. Применение нашего анализа к взаимным фондам или фондам фондов может быть неточным, поскольку они не несут явных транзакционных издержек, однако, включают неявные транзакционные издержки, возникающие при торговле отдельными ценными бумагами и фьючерсами, а также могут включать плату за выдачу и погашение.

Ссылки

Aliaga-Díaz, Roger, Giulio Renzi-Ricci, Ankul Daga, and Harshdeep Ahluwalia, 2019. Vanguard Asset Allocation Model: An Investment Solution for Active-Passive-Factor Portfolios. Valley Forge, Pa.: The Vanguard Group.

Buetow, Gerald W., Ronald Sellers, Donald Trotter, Elaine Hunt, and Willie A. Whipple, 2002. The Benefits of Rebalancing. The Journal of Portfolio Management 28(2): 23-32.

Chan, Lydia J., and Sunder R. Ramkumar, 2011. Tracking Error Rebalancing. The Journal of Portfolio Management 37(4): 54-66.

Czasonis, Megan, Prabodh Pradhan, and David Turkington, 2020. The Realities of Rebalancing: What Is the Best Approach? State Street Associates;
https://www.opiniopro.com/2020/04/state-street-global-advisors/the-realities-of-rebalancing/

Davis, Joseph, Roger Aliaga-Díaz, Harshdeep Ahluwalia, Frank Polanco, and Christos Tasopoulos, 2014. Vanguard Global Capital Markets Model. Valley Forge, Pa.: The Vanguard Group.

Davis, Joseph H., Qian Wang, Edoardo Cilla, and Kevin DiCiurcio, 2022 (forthcoming). Vanguard Global Capital Markets Model 4.0. Valley Forge, Pa.: The Vanguard Group.

De Juan, Michael, Laura A. Di Poce, and Daniel Phillips, 2018. Portfolio Rebalancing: How and How Often? Northern Trust;
https://www.northerntrust.com/documents/commentary/portfolio-rebalancing-strategy-commentary.pdf

Donohue, Christopher, and Kenneth Yip, 2003. Optimal Portfolio Rebalancing With Transaction Costs. The Journal of Portfolio Management 29(4): 49-63.

Harjoto, Maretno A., and Frank J. Jones, 2006. Rebalancing Strategy for Stocks and Bonds Asset Allocation. The Journal of Wealth Management 9(1): 37-44.

Jones, Samuel Kyle, and Joe Bert Stine, 2010. Expected Utility and the Non-Normal Returns of Common Portfolio Rebalancing Strategies. Journal of Asset Management 10(6): 406-419.

Kritzman, Mark, Simon Myrgren, and Sebastien Page, 2009. Optimal Rebalancing: A Scalable Solution. Journal of Investment Management 7(1): 9-19.

Masters, Seth J., 2003. Rebalancing. The Journal of Portfolio Management 29(3): 52-57.

Norges Bank Investment Management Discussion Note, 2012. Empirical Analysis of Rebalancing Strategies. March 30;
https://www.nbim.no/en/publications/discussion-notes/2012/empirical-analysis-of-rebalancing-strategies/

Plaxco, Lisa M., and Robert D. Arnott, 2002. Rebalancing a Global Policy Benchmark. The Journal of Portfolio Management 28(2): 9-22.

Sun, Walter, Ayres Fan, Li-Wei Chen, Tom Schouwenaars, and Marius A. Albota, 2006. Optimal Rebalancing for Institutional Portfolios. The Journal of Portfolio Management 32(2): 33-43.

Zilbering, Yan, Colleen M. Jaconetti, and Francis M. Kinniry Jr., 2015. Best Practices for Portfolio Rebalancing. Valley Forge, Pa.: The Vanguard Group.

Приложение

ВАЖНО: Прогнозы и другая информация, полученная в результате моделирования (аналогично VCMM) относительно вероятности различных результатов инвестирования, носят гипотетический характер, не отражают фактические результаты инвестиций и не являются гарантиями будущих результатов. Результаты модели будут меняться при каждом использовании и с течением времени.

Прогнозы основаны на статистическом анализе исторических данных. Будущие доходы могут вести себя иначе, чем зафиксированные исторические закономерности в модели. Что еще более важно, модель может недооценивать экстремальные негативные сценарии, не наблюдавшиеся в течение исторического периода, на котором основана оценка модели.

Модель представляет собой запатентованный инструмент финансового моделирования. Модель прогнозирует распределение будущих ежедневных доходов по широкому спектру классов активов. Эти классы активов включают американские и международные фондовые рынки, рынки казначейства США с несколькими сроками погашения и корпоративные рынки с фиксированным доходом, а также международные рынки с фиксированным доходом. Теоретическая и эмпирическая основа для модель заключается в том, что доходность различных классов активов отражает компенсацию, требуемую инвесторами за то, что они несут различные типы систематического риска (бета).

В основе модели лежат оценки динамической статистической взаимосвязи между факторами риска и доходностью активов, полученные в результате статистического анализа на основе доступных ежедневных финансовых и экономических данных. Используя систему расчетных уравнений, модель затем применяет метод моделирования методом Монте-Карло для прогнозирования расчетных взаимосвязей между факторами риска и классами активов, а также неопределенностью и случайностью с течением времени. Модель генерирует большой набор смоделированных результатов для каждого класса активов на нескольких временных горизонтах. Прогнозы получаются путем вычисления показателей центрального тренда в этих симуляциях. Результаты, полученные с помощью этого инструмента, будут меняться при каждом использовании и с течением времени.

Приложение А-1: Система принятия решений на основе полезности

Модель использует постоянное относительное неприятие риска (Constant Relative Risk Aversion, CRRA) — служебную функцию, как указано ниже:

Полезность (w) = w ^(1–r) / (1–r)

w = Конечный капитал портфеля (после учета транзакционных затрат)
r = Коэффициент неприятия риска

Описанная выше функция полезности CRRA учитывает неприятие инвестором риска, определяемое как неприятие инвестором неопределенности результатов. Инвестор, не склонный к риску, предпочитает низкую степень определенности. Инвестор с низкой нетерпимостью к риску терпимо относится к неопределенности ради лучшего результата. Наша модель может генерировать результаты с любым введенным пользователем коэффициентом неприятия риска. Итоговые оценки полезности в нашем анализе отрицательные, поскольку мы предполагаем, что конечный капитал портфеля всегда положительный (интуитивно капитал не опускается ниже нуля), а коэффициент неприятия риска инвестором больше единицы.

Vanguard

 

---

---

---

Комментариев нет »