 Уильям Бернстайн
Уильям Бернстайн
«Четыре столпа инвестиций»
Перевод для AssetAllocation.ru
СТОЛП ПЕРВЫЙ
Теория инвестиций
В 1798 г. французская экспедиция во главе с Наполеоном вторглась в Египет. Его войска располагали лишь самыми элементарными картами и почти ничего не знали о климате или местности. Неудивительно, что вторжение было катастрофой от начала до конца, когда три года спустя последние французские войска, подавленные, больные, голодающие и покинутые своим лидером, были уничтожены силами турков и британцев.
К сожалению, большинство инвесторов применяют похожую степень планирования к своим инвестициям, не осознавая природы инвестиционного ландшафта и климата. Без понимания взаимосвязи между риском и вознаграждением, принципами оценки доходности, взаимодействия между другими инвесторами и самими собой, а также механики формирования портфеля на протяжении примерно полувека среднего инвестиционного жизненного цикла, инвесторы обречены, подобно войскам Наполеона, на неудачу. В первом разделе книги, глава за главой, будет рассмотрена каждая из этих важных тем.
Часть 1
Кто не рискует, тот не выигрывает
Большую часть своей взрослой жизни я занимался медициной, и эти годы подтвердили распространенное мнение о том, что врачи – никудышные инвесторы.
Два фактора делают это почти неизбежным: во-первых, врачи в большей степени, чем большинство специалистов, страдают от чрезмерной самоуверенности; во-вторых, они не подходят к финансам с той же строгостью, что и к медицине. Не заблуждайтесь: финансы – такая же серьезная область для изучения, как и любая физическая, биологическая или социальная наука, и тем не менее почти никто за пределами финансов – и не только врачи – не тратит время на изучение их основ.
Вы ожидаете, что ваш врач не станет лечить вас даже от простуды без глубокого понимания физиологии, анатомии, патологии, фармакологии, обучения клинической практике и, наконец, постоянного наблюдения за рецензируемой медицинской литературой. Тем не менее, большинство врачей распоряжаются своими жизненными сбережениями, даже не взглянув на финансовые эквиваленты этих областей. С точки зрения медицины это похоже на изучение хирургии головного мозга путем чтения раздела о здоровье в USA Today.
ФИНАНСОВАЯ ТЕОРИЯ: ПРЕМИЯ ЗА РИСК
Финансовая версия физиологии – науки о том, как работает организм, – это финансовая теория. Если бы нужно было сформулировать это в одном предложении, оно звучало бы так: Доходность и риск неразрывно связаны; высокую доходность можно получить, только принимая на себя большие риски и время от времени терпя большие убытки, а безопасность достигается при низкой доходности.
Представьте, например, что Казначейство США выпускает бессрочную облигацию с доходностью 3%, то есть срок ее погашения никогда не наступает. Обычно номинальная стоимость одной облигации составляет $1000, поэтому проценты по ней приносят $30 в год. Теперь представьте, что вместо того, чтобы выплачивать по $30 в год, министр финансов подбрасывает монету: орел – проценты за этот год составят $60; решка – ноль.
В течение достаточно длительного периода ежегодные дивиденды по-прежнему будут составлять в среднем $30 в год. Однако инвесторы, недовольные ненадежностью выплат, соответственно оценят облигацию и снизят ее цену с $1’000, скажем, до $750, чтобы компенсировать необходимость терпеть эту неопределенность. При такой цене доходность вырастет с 3% до 4% ($30/$750). Говоря языком финансов, этот дополнительный 1% доходности – это «премия за риск», за неопределенность при подбрасывании монеты.
«Премия за риск» – один из наиболее важных терминов в этой книге. Премия за риск в размере 1% в предыдущем примере с облигациями с подбрасыванием монеты – примерно соответствует тому, что инвестор мог бы ожидать от облигации, выпущенной компанией с низким, но не нулевым риском банкротства.
Акции несут в себе еще больший риск, и, следовательно, имеют более высокую премию за риск. Чтобы представить его в общих чертах, я собираюсь вспомнить вышедшего на пенсию персонажа из книги «Разумное распределение активов», вашего мифического дядюшку Фреда, который также приходится вам работодателем.
Вскоре после того, как вы подписали с ним контракт, он отводит вас в сторону и знакомит с самым необычным пенсионным планом компании. В конце каждого года он вносит $5’000, а затем предлагает вам следующий выбор:
- Вариант 1: Вы получаете безопасную доходность в размере 3% от накопленной суммы.
- Вариант 2: Вы подбрасываете монету: орел – ваша заначка приносит доход в размере 30% за год; решка – она теряет 10%.
Вы собираетесь работать на дядю следующие 35 лет. Вы умеете работать с электронными таблицами и быстро подсчитываете, что при выборе варианта 1, когда вы выйдете на пенсию, у вас будет всего $302’310, чтобы прожить свои золотые годы. Хотя это может показаться кругленькой суммой, это не так. Если в течение следующих 35 лет инфляция сохранится на своем историческом уровне в 3%, у вас останется лишь $107’436 в текущей покупательной способности. (*)
Второй вариант, при котором вы с вероятностью 50/50 потеряете за год 10% своих сбережений, заставляет вас покрыться холодным потом. Что, если у вас впереди череда потерянных лет? Если все 35 лет у вас будет выпадать решка, то на пенсию вам могут остаться лишь гроши. С другой стороны, если все 35 лет у вас будет выпадать орел, вы знаете, что обанкротите бедного дядюшку Фреда своими доходами – он будет должен вам 162 миллиона долларов!
Конечно, оба этих результата исчезающе маловероятны: (1/2) в степени 35, или 0,000000003% в каждом случае. Но все равно можно выбрать первый, безопасный вариант, поэтому давайте более внимательно рассмотрим подбрасывание монеты. В течение достаточно длительного периода вы получите половину орлов и половину решек. Если представить это в виде чередующейся серии орлов и решек, то ваш доход за каждый двухлетний период будет представлен следующим образом:
1,3 × 0,9 = 1,17
Доходность в размере 30% за первый год приводит к тому, что ваш счет умножается на 1,3; а убыток в 10% во второй год — на 0,9. В конце этих двух лет у вас будет $1,17 на каждый доллар, с которого вы начали, что соответствует годовой доходности 8,17%, что дает ожидаемую премию за риск в размере 5,17% по сравнению с безопасной доходностью в 3% в варианте 1.
Вы еще немного играетесь со своей таблицей и обнаруживаете, что для выбора безопасного варианта с 3%, вам нужно получить 12 орлов и 23 решки либо хуже. Каковы шансы на это? Вы не уверены, поэтому посещаете своего бывшего профессора статистики из колледжа, который угощает вас своим запатентованным долгим печальным вздохом и указывает, что вы могли бы легко рассчитать шансы на любую комбинацию подбрасываний монеты с помощью так называемой функции биномиального распределения. Ваш пустой взгляд вызывает еще один вздох; затем он подходит к своему ноутбуку, запускает электронную таблицу и после нескольких быстрых нажатий клавиш выводит график на Рис. 1.1.
Рис. 1.1. Вероятность подбрасывания монеты дядюшкой Фредом
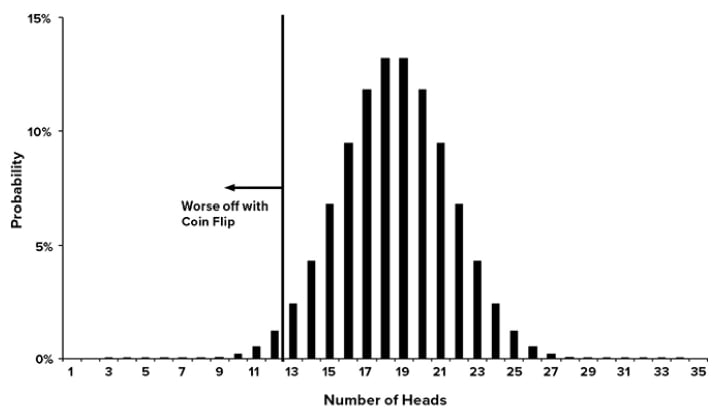
X – количество орлов; Y – вероятность; область слева – подбрасывание монетки хуже
Вы берете график и файл таблицы домой и выясняете, что вероятность того, что вы проиграете безопасному варианту 1, выбросив 12 орлов или менее, составляет менее 5%.
Параметры подбрасывания монеты дядюшкой Фредом выбраны не случайно. Я взял результаты +30%/−10% в год, чтобы получить результаты, похожие на среднегодовую доходность и волатильность (риск) широкого рынка акций США, а также премию за риск по акциям в размере 5,17% по сравнению с безопасной ставкой варианта 1, что примерно соответствует премии за риск акций по отношению к казначейским векселям не только в Соединенных Штатах, но и за рубежом. В среднем вы действительно преуспеете, выбирая подбрасывание монеты, но каждый год это сопряжено с захватывающим дух беспокойством, и все еще сохраняется небольшой шанс, что вы пожалеете, что не выбрали безопасный вариант.
| МАТЕМАТИЧЕСКИЙ БЛОК Геометрические доходности, арифметические доходности, отрицательное влияние дисперсии Некоторые из вас могут задаться вопросом, почему доходность подбрасывания монеты составляет не 10%, а 8,17% − ведь среднее значение между +30% и -10% составляет +10%? Средняя доходность – это просто среднее значение всех отдельно взятых годовых доходностей. Годовая доходность – более тонкое понятие. Это доходность, которую вы должны в среднем зарабатывать каждый год, чтобы итоговый результат оказался равен результату вашей серии различных годовых доходностей.Представьте, что у вас есть акция, которая в первый год удваивается в цене (приносит доходность 100%), а в следующем году теряет 50%. Если в начале акция стоила $10, тогда она стоила $20 в конце первого года, и вновь $10 в конце второго года. Вы заработали нулевую прибыль, однако средняя доходность составляет «25%» (среднее между +100% и −50%). Годовая (геометрическая) и средняя (арифметическая) доходности – явно не одно и то же: с точки зрения статистики последняя является средним значением, в то время как первая ближе к медиане. Подбрасывание монеты имеет среднюю (арифметическую) доходность 10% и годовую (медианную) доходность 8,17%. Годовая доходность всегда меньше средней доходности. Если подбрасывание монеты в половине случаев дает доход −10%, а в половине +30%, то это то же самое, что доходность 8,17% ежегодно. Вы оплачиваете свои счета с помощью годовой доходности, а не средней. Разница между средней и годовой доходностями составляет примерно половину дисперсии (квадрата стандартного отклонения), это так называемое отрицательное влияние дисперсии – штраф, который вы платите за высокую волатильность ценной бумаги или класса активов. Он приблизительно равен: [Геометрическая доходность] ≅ [Арифметическая доходность] – [Дисперсия/2] Если в вашем портфеле нет поступлений или оттоков средств, порядок подбрасывания монеты не важен. Но если вы добавляете или забираете средства, порядок доходностей имеет большое значение. Возьмем два экстремальных, но крайне маловероятных исхода подбрасывания монеты дядюшкой Фредом. Если вы будете каждый год добавлять одну и ту же сумму и выпадет 16 орлов, а затем 19 решек, вы все равно окажетесь ниже 3%-ной безопасной доходности варианта 1. Но если вы выбросите подряд 27 решек, а затем подряд 8 орлов, вы фактически опередите вариант 1. Это, конечно, крайне маловероятные события, используемые только для иллюстрации того, что порядок доходностей в действительности имеет значение, поэтому Рис. 1.1, хотя и является упрощением, по-прежнему достойно отражает шансы в вашу пользу. Почему порядок результатов подбрасывания монеты имеет значение? Потому что последовательность из 27 решек, за которой следует последовательность из 8 орлов, позволяет получить более высокую доходность на более поздних этапах с наибольшей суммой денег, что компенсирует низкую доходность на ранних этапах. Это означает, что молодому человеку, который активно откладывает пенсионные накопления, лучше получить низкую доходность портфеля вначале, и высокую доходность позже. Чуть далее в книге я объясню, почему верно и обратное утверждение: пенсионеру лучше получить хорошую доходность сразу, а плохую – позже, и что это означает для распределения активов при выходе на пенсию. |
ЗА ПРЕДЕЛАМИ ПОДБРАСЫВАНИЯ МОНЕТЫ
Я представил подбрасывание монеты дядюшкой Фредом как простой способ проиллюстрировать связь между риском и доходностью облигаций и акций; первые представлены постоянной доходностью 3% в варианте 1, а вторые – подбрасыванием монеты с премией за риск 5,17% (8,17% – 3,00%). Оба варианта были разработаны чтобы приблизиться к реальному миру акций и казначейских векселей. Но откуда на самом деле берутся эти доходы и риски? Чтобы понять это, нам нужно изменить точку зрения с точки зрения инвестора на точку зрения человека, которому нужны деньги для начала или развития бизнеса.
С момента зарождения денежной экономики в древнем мире существовало лишь два способа финансирования бизнеса: долг или акционерный капитал – в современном мире большого бизнеса и крупных финансов это облигации и акции.
Представьте, что вы – подающий надежды шеф-повар ближневосточной кухни, которому нужно $10’000, чтобы установить тележку с едой в вашем районе. Ваш первый выбор – занять деньги у кого-нибудь. Предположим, что ни у вас, ни у ваших друзей и родственников нет таких денег, и вы вынуждены обратиться в банк за кредитом.
Давайте далее предположим, что вы предлагаете банку свою тележку в качестве залога, что она стоит $12’000, и что у вас достаточно денег, чтобы компенсировать разницу в $2’000 между суммой кредита и ценой покупки. С точки зрения банка, кредит является предложением с относительно низким уровнем риска: если ваш бизнес преуспеет, то банк вернет основную сумму кредита в размере $10’000 плюс проценты, а если вы потерпите неудачу, он конфискует тележку, стоимость которой более чем окупит сумму кредита. Из-за относительно низкого риска, обеспечиваемого залогом, банк возьмет с вас разумную процентную ставку – вероятно, в пределах от 6% до 10%. Увы, с вашей точки зрения, такое долговое финансирование в действительности сопряжено с очень высоким риском: если вы потерпите неудачу, то обанкротитесь.
Альтернативный способ пополнить тележку с едой – предложить долю в капитале подруге, назовем ее Сью, которая попробовала вашу шаурму и думает, что другие сочтут ее неотразимой. В обмен на $10’000 вы передадите ей половину владения бизнесом.
Соотношение рисков инвестора и бизнесмена теперь меняется на противоположное. С точки зрения Сью ее инвестиции крайне рискованны; если ваш бизнес по любой причине потерпит неудачу – возможно, соседи не так любят острую пищу, они пожалуются в муниципалитет, пандемия прервет цепочку поставок ресторанных принадлежностей и ингредиентов либо ваш участковый наконец поймает вас – она теряет все свои инвестиции. Финансовые чудаки называют Сью «остаточным владельцем» вашей тележки с едой: как управляющий вы не обязаны выплачивать какую-либо прибыль от его работы (в мире акций это дивиденды) себе и Сью, а если захотите, то можете снизить или прекратить выплату прибыли себе и Сью. Потенциал роста прибыли теоретически безграничен, и даже есть крошечный шанс, что через 10 лет Сью станет совладелицей международного конгломерата быстрого питания. И наоборот, с вашей точки зрения, продажа ей доли (акций) в вашем ларьке с шаурмой снижает ваш риск, поскольку неудача не приведет вас к банкротству.
С другой стороны, в случае банковского кредита весь риск ложится на вас; если вы не сможете выплатить основную сумму долга и проценты, то юридически станете банкротом, и в этом случае банк получит право первого требования на активы ларька.
Подводя итог: вы можете финансировать свой бизнес с помощью кредита, что рискованно для вас и является относительно безрисковым вариантом для кредитора (подумайте о «владельце облигаций»), либо можете финансировать его за счет акционерного капитала, что представляет собой высокий риск для владельца капитала, но меньший риск для вас. Поскольку Сью, как владелица акций, принимает на себя больший риск, чем банк, она заслуживает премии за риск по акциям. В следующей таблице суммированы отношения риска между инвестором и предпринимателем при долговом и долевом финансировании.
Инвестор: долг – низкий риск; доля – высокий риск
Предприниматель: долг – высокий риск; доля – низкий риск
И последнее замечание: на самом деле Сью не обязательно иметь деньги, необходимые для инвестиций в ваш ларёк; она может занять их. В этом случае она совершает не одну рискованную вещь, а две: занимает деньги и инвестирует в акционерный капитал. В финансовом мире это то же самое, что инвестировать в акции с высокой маржой, что рано или поздно увеличивает вероятность того, что ваш инвестиционный автомобиль соскользнет с шоссе богатства в кювет.
Вечный вопрос, связанный с личными инвестициями, заключается в том, использовать ли ваши деньги для погашения ипотеки, либо использовать деньги банка для пополнения своего инвестиционного портфеля. Вкладывать эти деньги в облигации часто неразумно, поскольку ваша ипотечная ставка обычно будет значительно выше процентной ставки по облигациям. Что еще более важно, вкладывать ипотечные деньги в акции еще менее разумно, поскольку ваша ипотека фактически становится маржинальным кредитом, хотя и не может, как в случае с брокерским счетом, быть отозвана и привести к тому, что ваш брокер невольно продаст ваши акции, если их цены серьезно упадут. Так что погасите ипотеку, если сможете: в следующий раз, когда экскременты попадут в систему вентиляции, вы будете спать лучше.
ЕЩЕ ОДИН ВАЖНЫЙ ТЕРМИН: ОЖИДАЕМАЯ ДОХОДНОСТЬ
«Премия за риск» – относительно простая для понимания концепция; иначе обстоит дело с гораздо более скользким вопросом: «ожидаемой доходностью» (expected return).
Одному богу известно, будет ли успешным ваш ларек с шаурмой. Предположим, что существует 40%-ная вероятность того, что в течение следующих 10 лет дела у него будут идти хорошо, и что вы потратите всю его прибыль на то, чтобы превратить его в модный ресторан, который можно будет продать за $200’000. В этом случае Сью получит половину – $100’000. Далее предположим, что остается 60%-ная вероятность того, что все пойдет прахом; если мы взвесим каждый из двух возможных исходов для Сью – либо $100’000, либо ноль – по их вероятностям, то увидим, что ожидаемый выигрыш Сью составит $40’000 (0,4 × $100’000 плюс 0,6 × $0).
Ожидаемое увеличение денег Сью в четыре раза за 10 лет приводит к ожидаемой доходности в 14,9% годовых. (**) Эта высокая ожидаемая доходность, конечно, звучит привлекательно, но высокая ожидаемая доходность всегда сопряжена с риском, в данном случае с вероятностью 60%, что Сью потеряет все до последнего пенни; этот дополнительный риск является причиной того, что акции предлагают более высокую ожидаемую доходность, чем безопасные активы: «премию за риск акций».
КАК МЫ ОЦЕНИВАЕМ ОЖИДАЕМУЮ ДОХОДНОСТЬ АКЦИЙ?
В реальном мире компании напоминают живые организмы: они рождаются, могут расти, а могут и не расти, а затем умирают. Большинство животных живут очень короткий промежуток времени, в то время как некоторые, такие как гренландская акула, могут прожить три столетия, а некоторые виды беспозвоночных и деревьев, такие как щетинистая сосна, выживают в течение тысячелетий.
Точно так же лишь около половины малых предприятий доживают до 5 лет, а период полураспада публично торгуемых компаний составляет около 10 лет. Некоторые небольшие частные американские предприятия действовали еще до Войны за независимость, а некоторые, например, две крупные корпорации, основанные Дж. П. Морганом – General Electric и US Steel, – торгуются на фондовых биржах уже более столетия.
Поскольку большинство компаний исчезают, почти все, что они оставляют своим инвесторам, – это дивиденды, которые они (или компании, которые их поглощают или сливаются с ними) выплачивают перед смертью; это единственный правильный способ оценить акции. В настоящее время, например, Facebook/Meta Platforms не выплачивает дивиденды; если ей удастся обанкротиться или быть закрытой правительством до того, как это произойдет, она принесет своим конечным инвесторам одни убытки. (Исключением из правила «все компании умирают и не оставляют ничего, кроме дивидендов» является случай обратного выкупа акций, который обеспечивает лишь небольшую часть общей доходности фондового рынка.)
Самый простой способ понять ожидаемую доходность акций – представить себе мифический фондовый рынок, который всегда приносит совокупные дивиденды в размере 3%, и чьи дивиденды растут с постоянной скоростью 5% в год. Начнем с цены акций фондового индекса в $100 и дивидендов в $3. В следующем году дивиденды вырастут на 5% до $3,15, поэтому цена индекса также должна увеличиться на 5% до $105, чтобы сохранить доходность постоянной на уровне 3% ($3,15/$105,00 = 3%). Теоретически, каждый год вы получаете 3% дивидендов и 5% роста цен: итого 8% (при условии, что дивиденды не реинвестируются). Это простое арифметическое соотношение…
Ожидаемая доходность = Дивидендная доходность + Рост дивидендов
… называется уравнением Гордона; оно должно быть в голове у любого долгосрочного инвестора.
СЕКС, ЛОЖЬ И СТАВКА ДИСКОНТИРОВАНИЯ
Давайте вернемся к двум мифическим казначейским облигациям из начала главы, срок погашения которых никогда не наступает, с бессрочными купонными выплатами по $30 в год. При этом по первой выплачиваются регулярные $30 ежегодно, а по второй выплачивается купон, определяемый подбрасыванием монеты: $60 или $0.
Напомним также, что мы начали с цены первой облигации в $1’000 и доходности 3%, то есть годового купона в $30. Но есть способ взглянуть на эту мифическую облигацию получше: обратить процесс вспять и спросить, а какую ставку дисконтирования мы применяем к этому купону в размере $30 в год, чтобы получить рыночную цену? Если мы применим к нему ставку дисконтирования 3%, то получим $30/3% = $1’000. А поскольку вторая облигация с выплатой процентов по принципу «подбрасывание монеты» является более рискованной, мы применяем к ней более высокую ставку дисконтирования: 4%. Таким образом, поток дохода оценивается в 30/4% = $750.
Это подводит нас к главной истине инвестирования: реальная стоимость ваших активов – это не цифры в вашем брокерском отчете, а поток дохода, который они обеспечивают. В случае облигаций – выплаты купонов, а в случае с акциями – выплаты дивидендов. Или, что более романтично, ваш собственный кусочек экономики.
В этом отношении британцы имеют преимущество перед американцами в несколько столетий. До недавнего времени, если бы вы спросили кого-нибудь из Соединенного Королевства о чьем-либо чистом капитале, наиболее вероятный ответ был бы примерно таким: «Она зарабатывает около $20’000 в год». Американцы, напротив, влюбляются в цифры в своих брокерских отчетах. Проблема в том, что, как вы можете видеть из предыдущего расчета, они чрезвычайно чувствительны к знаменателю ставки дисконтирования, который растет и падает в зависимости от восприятия риска рынком. Например, во время мирового финансового кризиса финансовые рынки решили резко увеличить учетную ставку, что оказало обратное влияние на цены.
Обратное происходит во время биржевых маний, когда рынок решает применить гораздо более низкую ставку дисконтирования. Возможно, самым ярким примером этого явления была книга Джейма Глассмана и Кевина Хассетта, «Доу 36’000». На момент публикации книги в 1999 г. рынок, казалось, применял примерно 9%-ную ставку дисконтирования к будущим доходам фондового рынка, что отражалось в уровне индекса Доу-Джонса, который составлял на тот момент около 10’000 пунктов.
Чепуха, сказали авторы, инвесторы скоро придут к пониманию того, что акции вовсе не являются рискованными в долгосрочной перспективе, и, таким образом, применят гораздо более низкую ставку дисконтирования в размере 3% к своим будущим дивидендам, что утроит цену в течение нескольких лет. (1) Излишне говорить, что этого не произошло. Индекс Доу-Джонса действительно временно достиг 36 000 пунктов – 22 года спустя, и не раньше, чем по ходу дела дважды упал примерно вдвое. Основываясь на историческом росте цен на акции на 6% в год, я бесстрашно прогнозирую рост индекса Доу-Джонса до $100’000 в 2040 г.
| МАТЕМАТИЧЕСКИЙ БЛОК Уравнение Гордона, риск и ставка дисконтирования Предыдущее повествовательное объяснение уравнения Гордона скрывает за собой более сложную математику, центральным элементом которой является ставка дисконтирования. Допустим, кто-то предлагает вам на выбор чизбургер на обед сегодня или более одного чизбургера через 10 лет. Сколько из них стоили бы того, чтобы подождать? Допустим, вы хотите два; таким образом, ваша ставка скидки на чизбургеры составляет 2 в степени 0,1 – 1 = 7,2%, что соответствует ставке сложных процентов, необходимой для удвоения количества ваших чизбургеров за 10 лет. (Это легко понятный пример «правила 72»: процентная ставка, умноженная на время удвоения, приблизительно равна 72 [7,2 × 10]; срок удвоения при процентной ставке 12% составляет 6 лет. Люди плохо умеют вычислять экспоненциальные зависимости, и «правило 72» – хороший способ справиться с этим недостатком. Допустим, вы вышли на прогулку без калькулятора в кармане, и вам пришло в голову прикинуть, на сколько вырастет доллар за 50 лет при 10%-ной доходности. Это означает, что он удваивается примерно раз в 7 лет; за 50 лет он удвоится примерно семь раз, или до $128 долларов — как в последовательности $2, $4, $8, $16, $32, $64, $128 – что приближает вас к реальному ответу $117,39.). Теперь предположим, что человек, предлагающий вам сделку, очень стар или ненадежен и может не прийти, чтобы расплатиться за чизбургеры. В этом случае, чтобы компенсировать риск того, что вы их не получите, вам захочется больше чизбургеров – скажем, 5. И в этом случае ваша ставка дисконтирования на чизбургеры теперь намного выше: 5 в степени 0,1 – 1 = 17,5%.Таким образом, ставка дисконтирования – это доходность, которую вы требуете для компенсации риска владения активом, и это хороший способ понять тесную связь между риском и доходностью.Предположим, что компания выплачивает поток дивидендов, который растет со скоростью g и простирается на неопределенное время в будущее, и что эти дивиденды дисконтируются на ожидаемую доходность r, в этом случае сегодняшняя цена компании P0 представляет собой бесконечную сумму всех будущих дивидендов: P0 = ∑ D0 × ((1 + g)t / (1 + r)t) Финансовые экономисты называют эту формулу «моделью дисконтирования дивидендов». Обратите внимание, что темп роста дивидендов g не может быть больше ставки дисконтирования r, поскольку это сделало бы стоимость компании сегодня бесконечной. Если мы применим некоторые математические вычисления к предыдущей формуле, чтобы найти r, ставку дисконтирования/ожидаемую норму прибыли, то получим: R = D1 + g Это простое уравнение почти идентично упрощенному уравнению, которое мы вывели ранее в описательной форме, за исключением того факта, что D1 – это дивиденд следующего года, деленный на сегодняшнюю цену. D1 заменяет сегодняшнюю дивидендную доходность, D0 в упрощенном уравнении – достаточно близко для наших целей. |
ОТ ОЖИДАЕМОЙ ДОХОДНОСТИ К РЕАЛИЗОВАННОЙ ДОХОДНОСТИ, ИЛИ ВАЖНОСТЬ «РЕАЛЬНОГО» ОТНОШЕНИЯ К ИНФЛЯЦИИ
Те из вас, у кого острый глаз, наверняка заметили, что, хотя я только что сказал вам, что все компании рано или поздно умирают, я по-прежнему предполагаю, что прибыли и дивиденды рынка в целом сохранятся на неопределенный срок в будущем. Это связано с тем, что гораздо менее вероятно, что весь фондовый рынок страны погибнет. Иногда такое случается, но, когда это происходит, у вас возникают гораздо более серьезные проблемы, чем ваш пенсионный портфель.
Насколько хорошо уравнение Гордона помогает предсказать доходность фондового рынка в целом? В настоящее время около 3’500 компаний США торгуются на фондовых биржах, и доступны очень качественные данные об их доходностях с 1926 г. Давайте представим, что в тот год вы были инвестором, который хотел оценить долгосрочную будущую доходность. Как бы вы это сделали?
Давайте поставим себя на место этого инвестора 1 января 1926 г. В течение последнего полувека акции приносили около 5,0%, а дивиденды росли примерно на 1,6% в год. Разумный инвестор предсказал бы доходность в размере 5,0% + 1,6% = 6,6% в будущем.
Хотя сегодняшний инвестор сразу же заволновался бы о том, как инфляция подорвет эту доходность, в 1926 г. это не вызывало особого беспокойства, поскольку за предшествовавшие полвека инфляция в годовом исчислении составляла лишь около 0,7%. Эта инфляция на уровне 0,7% снизила ожидаемую доходность с поправкой на инфляцию до 5,9%. Фактически, с 1926 г. по конец 2021 г. индекс S&P 500 прибавил 7,35% после вычета инфляции, что на 1,45% выше, чем прогнозировалось уравнением Гордона.
Начиная с этого места в книге, мы будем говорить о вашем будущем личном потреблении товаров и услуг, богатстве и доходности инвестиций, главным образом, с поправкой на инфляцию, или в «реальном» выражении, поэтому внимательно следите за словом «реальный». К этому нужно немного привыкнуть. Например, за прошедшее столетие казначейские векселя США, которые большинство специалистов по финансам считают предпочтительным безопасным активом, приносили доходность 3,26% в год в сравнении с инфляцией в 2,90%, таким образом, принося лишь малую толику реальной доходности. Другими словами, доллар, вложенный в Казначейские векселя, в среднем лишь немного опережал цены на товары, которые вы хотите купить.
Почему произошел разрыв в 1,45% между ожидаемой реальной доходностью в 5,9%, рассчитанной в 1926 г., и реальной доходностью в 7,35%, реализованной в последующие 96 лет? Дело в том, что за эти 96 лет дивидендная доходность упала с 5,0% до 1,26%. Другими словами, в 1926 г. для получения $1 дивидендов требовалось покупка акций всего на $20. К началу двадцать первого века акции стали стоить намного дороже. В конце 2021 г. вам пришлось бы купить акций почти на $80, чтобы получить тот же $1 дивидендов. Таким образом, «дивидендный мультипликатор» увеличился почти в четыре раза, что за 96 лет с 1929 по 2021 гг. в годовом выражении привело к увеличению на 1,45% в год, что точно объясняет этот разрыв.
Итак, давайте добавим еще один член в уравнение Гордона, чтобы оно давало реализованную доходность – доходность, который вы действительно получили:
Реализованная доходность = Дивидендная доходность + Рост дивидендов + Годовое изменение дивидендного мультипликатора
Первые два слагаемых в предыдущем уравнении, дивидендная доходность плюс рост дивидендов, «ожидаемая доходность», также называются «фундаментальной доходностью» рынка – то, что вы получите, если мультипликатор дивидендов не изменится. Предыдущее уравнение упрощается до:
Реализованная доходность = Ожидаемая (фундаментальная) доходность + Годовое изменение дивидендного мультипликатора
Ожидаемая (фундаментальная) доходность – легко вычисляемое значение, и, что более важно, более стабильное. С другой стороны, годовое изменение мультипликатора, как мы вскоре увидим, колеблется, иногда резко и совершенно непредсказуемо и, следовательно, неизвестно. Лучше назвать его «спекулятивной доходностью». В разговорной речи мы можем резюмировать все это так:
Фактическая доходность = Фундаментальная доходность + Спекулятивная доходность
В любой конкретный день или даже в любой конкретный год спекулятивная доходность (изменение мультипликатора) превышает фундаментальную доходность. Например, в 2008 году дивидендный мультипликатор, а вместе с ним и спекулятивная доходность, упали на 42%, а в 1933 г. они выросли на ошеломляющие 66%, тогда как фундаментальная доходность за оба года изменилась всего на несколько процентов.
Даже за 10-летние периоды реальная годовая доходность может сильно отклоняться от оценки по уравнению Гордона, полученной на основе начальной дивидендной доходности S&P и долгосрочных темпов роста реальных дивидендов в двадцатом веке на уровне 1,46%, как показано на Рис. 1.2.
Рис. 1.2. Десятилетняя доходность S&P 500 с поправкой на инфляцию, предсказанная уравнением Гордона, в сравнении с фактической доходностью.
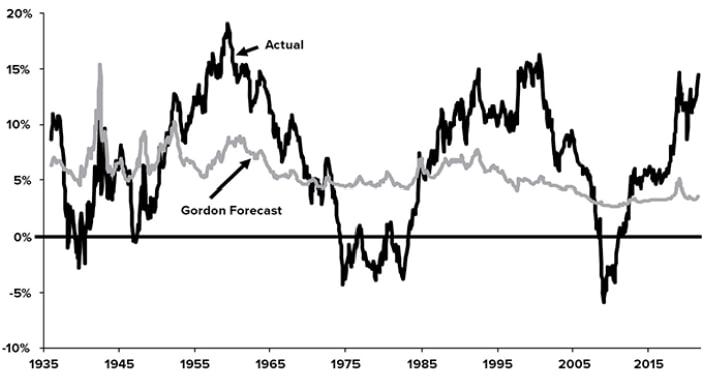
Темный график – фактическая доходность, светлый – предсказанная уравнением Гордона
Только в течение очень длительных периодов времени, порядка одного поколения, уравнение Гордона дает достаточно точную оценку будущих доходностей, как показано на Рис. 1.3.
Рис. 1.3. Тридцатилетняя доходность S&P 500 с поправкой на инфляцию, предсказанная уравнением Гордона, в сравнении с фактической доходностью
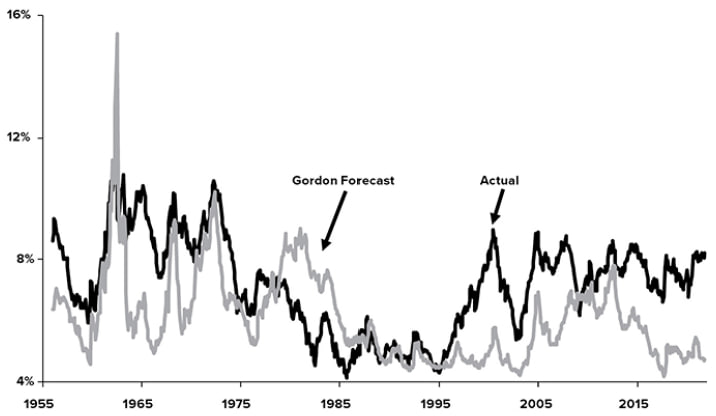
Темный график – фактическая доходность, светлый – предсказанная уравнением Гордона
Рис. 1.4 в упрощенном виде иллюстрирует относительную важность фундаментальной и спекулятивной доходности.
Рис. 1.4. Сигнал vs. шум: фундаментальная (ожидаемая) и спекулятивная (изменение мультипликатора) доходности с течением времени
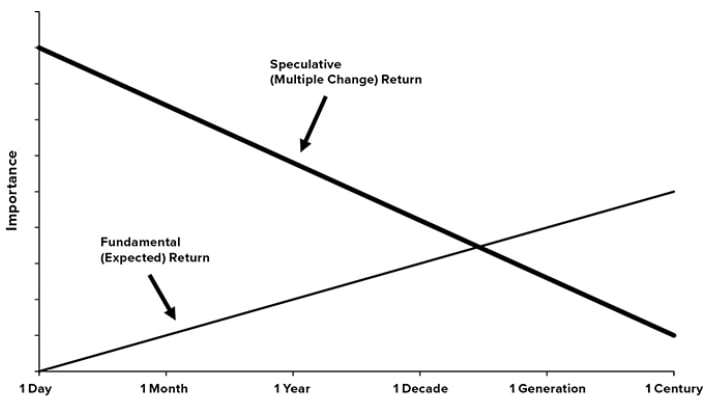
Темный график – спекулятивная доходность (изменение мультипликатора), светлый – фундаментальная (ожидаемая) доходность;
X – период (1 день / 1 месяц / 1 год / 1 декада / 1 поколение / 1 век); Y – важность
Даже за почти столетний период между концом 1925 и 2021 гг. (это даже дольше, чем инвестиционный горизонт г-жи Блум) впечатляющий четырехкратный рост дивидендного мультипликатора по-прежнему составлял пятую часть общей реальной доходности акций (1,45% из 7,35%).
Что это говорит нам об ожидаемой доходности с поправкой на инфляцию в будущем? Начнем с дивидендной доходности в 1,7% на конец 2022 г. Реальный рост дивидендов с 1926 г. составлял около 2,0% в год. Если мультипликатор не изменится, мы можем ожидать реальную доходность акций в размере 1,7% + 2,0% = 3,7%. (***)
Но даже в течение очень длительных периодов времени реализованная совокупная доходность может сильно колебаться. Например, в конце 2022 г. 30-летняя годовая реальная доходность индекса S&P 500 составляла 7,0%, в то время как прогноз по уравнению Гордона, сделанный 30 лет назад, в конце 1992 г., составлял 4,8%. Это не кажется очень большой разницей, но в совокупности за 30 лет эта разрыв в 2,2% приводит к почти двукратной разнице в конечном благосостоянии.
В лучшем случае уравнение Гордона позволяет получить приблизительную оценку на очень длительных периодах, но из-за «чуда сложных процентов» отклонение годовой доходности даже на несколько процентов может привести к большим различиям в конечном богатстве, фактически достигнутом за несколько десятилетий инвестиционной карьеры.
Окончание следует…
Другие записи:
Комментариев нет »







