Инвестиционные стратегии 21 века – 4. Кусочек бесплатного обеда

Фрэнк Армстронг
Investor Solutions
Перевод для AssetAllocation.ru
Оглавление

Глава 4
Кусочек бесплатного обеда

Потратьте немного времени, чтобы побродить по Чикагскому университету, и вы, вероятно, заметите спортсменов в необычных футболках. Кажется, что они расписаны вручную, небрежным почерком. Если вы спросите, вам ответят, что это подписи всех преподавателей, которые были удостоены Нобелевской премии!

Университет является институтом мирового класса во многих областях исследований, но в области финансов и экономики он полностью доминирует. Никакая другая организация не стоит даже близко.

Вы также можете заметить футболки, украшенные надписью TANSTAAFL («there ain’t no such thing as a free lunch» — «бесплатных обедов не бывает»). TANSTAAFL в Чикаго — больше чем религия. Бесплатные обеды выявляются и искореняются со страстью и убежденностью инквизиции. В Чикаго очень любят обсуждать тех, кто был замечен в участии в бесплатных обедах, истинный выпускник Чикаго будет до смерти отрицать, что когда-либо был, или даже мог быть на бесплатном обеде. Инвесторам во всем мире предлагается принять TANSTAAFL как свое личное кредо. Остерегайтесь продавцов, предлагающих бесплатные обеды!

Гарри Марковиц — очень яркая звезда в галактике суперзвезд Чикаго. Его докторская диссертация заложила основы Современной Портфельной Теории (СПТ) и произвела революцию в мире финансов. История гласит, что Марковиц написал эту работу за один день в библиотеке Чикагского университета в 1952 году. Позже она была отредактирована, расширена и опубликована в журнале под названием Portfolio Selection («Выбор портфеля»). И именно за нее Марковиц получил Нобелевскую премию по экономике в 1990 году.

По иронии судьбы, статья Марковица практически не помогла ему в получении докторской степени. У комиссии возникли серьезные сомнения в том, относится ли эта статья к области «чистой» (теоретической) экономики! Эту и многие другие истории об основателях современных финансов и их вкладе в науку, вы можете найти в книге Capital Ideas /«Фундаментальные идеи финансового мира. Эволюция», автор — Питер Бернстайн, прим. переводчика/ в моей библиотеке.

Ниже приводится упрощенное описание СПТ (Современной Портфельной Теории). Я не ставлю целью превратить вас в экономиста, но хочу показать, как инвесторы могут использовать СПТ для управления рисками. Если вы интересуетесь областью финансов и хотите получить дополнительные сведения об СПТ, я советую вам обратиться к первоисточнику и прочитать статью Марковица Portfolio Selection. Статья вполне понятная, даже для тех из нас, кто сомневается в своих способностях к математике. Марковиц оказывает большую услугу, чередуя текст с математическими расчетами.

Марковиц начинает с предположения, что все мы стремимся избежать риска. Он определяет «риск» как стандартное отклонение ожидаемой доходности. Однако, вместо того, чтобы измерять риск на уровне отдельных ценных бумаг, он считает, что риск должен измеряться на уровне портфеля: любые отдельные инвестиции следует рассматривать не с точки зрения их индивидуального риска, а с точки зрения вклада, который они вносят в совокупный портфель.

Теперь сделаем большой шаг вперед: в дополнение к двум измерениям инвестиций, риску и доходности, Марковиц включает в рассмотрение степень, с которой инвестиции, как ожидается, будут изменяться в одном направлении. Третье измерение — это корреляция инвестиций друг с другом (или их взаимное изменение).

Хотя Марковиц рассматривал взаимодействие отдельных ценных бумаг в портфеле, в настоящее время многие советники используют методы СПТ с классами активов вместо отдельных акций, чтобы построить глобально диверсифицированный портфель.

Корреляция — это очень простая концепция. Если инвестиции на каждом шаге всегда движутся вместе, то они имеют идеальную корреляцию, соответствующую значению «+1». Если они всегда движутся в противоположных направлениях, то они имеют идеальную отрицательную корреляцию, и это значение «–1». Если вы ничего не можете сказать о движении инвестиций по отношению друг к другу, то они не имеют корреляции, что оценивается значением «0». Конечно, два актива могут иметь любую корреляцию в интервале от «+1» до «–1» по отношению друг к другу.

К примеру, многие факторы оказывают влияние сразу на все авиакомпании. Процентные ставки, стоимость рабочей силы, безопасность полетов, сборы аэропортов и расходы на топливо означают одно и то же для American, Delta, и United. Мы можем ожидать, что цены их акций будут, как правило, двигаться вместе в рамках рыночного цикла. В самом деле, цены акций часто движутся вместе. Они очень тесно коррелированы.

Часто факторы, которые хороши для одной отрасли, плохи для другой. Взгляните на нефтяные компании и авиакомпании. Топливо — это значительные расходы для авиакомпаний. Если цена на топливо растет, можно ожидать, что нефтяные компании будут в прибыли, а авиакомпании пострадают. В результате, цены на их акции должны двигаться в противоположных направлениях. Зачастую так и происходит. Они имеют низкий или отрицательный коэффициент корреляции.

Как мы можем использовать это знание?

Представьте себе, что мы можем найти где-то в мире одну высокорискованную и высокодоходную инвестицию. Ее прохождение через рыночные циклы может выглядеть следующим образом:

Рис. 4.1. Рискованная инвестиция A
15% доходность — 50% риск (СО)

Представим также, что где-то есть другая высокодоходная и высокорискованная инвестиция. Эта вторая инвестиция имеет идеальную отрицательную корреляцию с первой. Каждый раз, когда первая идет вверх, вторая идет вниз, и наоборот.

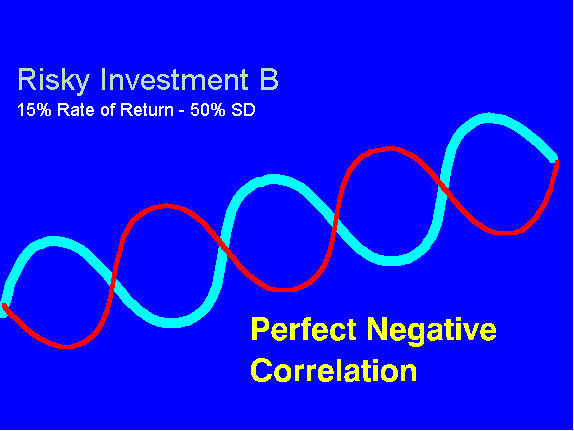
Рис. 4.2. Рискованная инвестиция B
15% доходность — 50% риск (СО)
Идеальная отрицательная корреляция

Если сложить их в портфель, то совокупный портфель будет иметь высокий доход и нулевой риск!

Краткосрочные выгоды одного вложения точно компенсируют потери в другом, а поскольку восходящий тренд обеих инвестиций имеет высокую доходность, их комбинация также имеет высокую доходность.

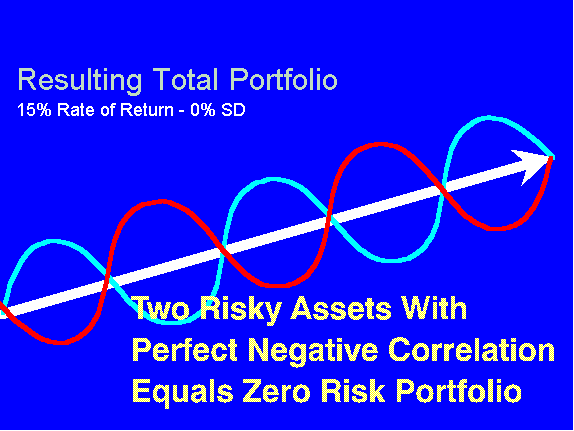
Рис. 4.3. Совокупный итоговый портфель
15% доходность — 0% риск (СО)
Два рискованных актива с идеальной отрицательной корреляцией
эквивалентны безрисковому портфелю

Спустимся с небес на землю. В реальном мире мы никогда не найдем два актива с идеальной отрицательной корреляцией. Однако хорошая новость состоит в том, что нам это и не нужно. Любая корреляция, которая ниже, чем идеальная положительная корреляция, снижает риск портфеля! Риск не будет полностью исключен: бесплатных обедов не бывает! Но, возможно, Современная Портфельная Теория предлагает инвесторам обед со скидкой. Либо кусочек бесплатного обеда!

Выводы из этого ошеломляют. Инвесторы впервые получили возможность строить портфели без оглядки на старую зависимость «риск-прибыль». В математических терминах, доходность портфеля равна средневзвешенной доходности вложений, но риск может оказаться ниже средневзвешенного по портфелю значения!

Мы подошли к моменту, когда пора сделать вывод: хотя большинство диверсификаций приносят пользу, некоторые из них лучше, чем другие. Мы получим больше пользы от диверсификации, включив в наш портфель авиакомпанию и нефтяную компанию, чем при включении двух авиакомпаний. Классическая диверсификация снижает риск бизнеса. Но диверсификация в том смысле, как она используется в СПТ, может реально способствовать снижению рыночного риска. В идеале мы хотим найти инвестиции, которые сочетают привлекательные характеристики «риск-прибыль» и низкую корреляцию с другими нашими инвестициями.

Нужно высказаться ясно. Я не ищу вложений, которые просто дают шанс потерять деньги, в то время как все другие вложения делают деньги. По мне так это просто еще одна глупая инвестиция. Я думаю, что каждая инвестиция в портфелях моих клиентов должна способствовать ожидаемой прибыли.

Есть еще одна (возможно, даже рациональная и разумная) точка зрения. Многие практики включают в портфель такой актив, как золото, из-за его низкой корреляции с другими классами активов. Это, возможно, безупречная точка зрения. И, возможно, этот подход приводит к снижению риска портфеля. Я смотрю на низкий 20-летний уровень доходности золота в сочетании с высокой волатильностью (риском), и принимаю решение не тратить проценты моего портфеля на этот актив.

Математика оказывается очень трудоемкой, поскольку для каждой инвестиции мы должны учесть ожидаемую доходность, риск, и корреляцию с любой другой инвестицией, которую мы рассматриваем. Количество необходимых данных растет в геометрической прогрессии по мере увеличения числа возможных вложений. Хуже того, даже всего для двух активов мы должны рассмотреть бесконечное число возможных портфелей. Я оставляю математикам решать, что происходит, когда потенциальное количество активов в портфеле становится более двух. От такого рода головоломок у меня всегда болит голова. Ответ может оказаться ближе к Дзен, чем к математике. В любом случае, такая математика не может быть просчитана без мощных быстродействующих компьютеров.

Марковиц изложил математику в своей работе в 1952 году, и большинство людей думали, что он решил задачу. Но Марковицу пришлось ждать более 20 лет — до середины 1970-х — чтобы получить доступ к ЭВМ и доказать, что он был прав. Впоследствии Марковиц признавался, что именно это был самый счастливый день в его жизни, а вовсе не тот день, когда он получил Нобелевскую премию! В то время один запуск оптимизационной задачи на ЭВМ стоил столько же, сколько новый автомобиль. Сегодня возможности вычислительных мощностей изменились. Вы можете сделать то же самое, к примеру, на старых ПК с процессором 8088.

В портфеле с определенным количеством активов лишь одна возможная комбинация позволяет добиться максимальной отдачи для каждого размера риска, который мы можем принять. Марковиц назвал это оптимальное сочетание вложений «эффективным». Любая другая комбинация вложений приведет к более низкому доходу при том же уровне риска. Эти уступающие комбинации являются менее эффективными. Если мы нанесем на график эффективные портфели для каждого уровня риска, то в результате получим линию наилучшего сочетания, которая называется «границей эффективности». К счастью, граница эффективности располагается выше прежней прямой риск-прибыль.

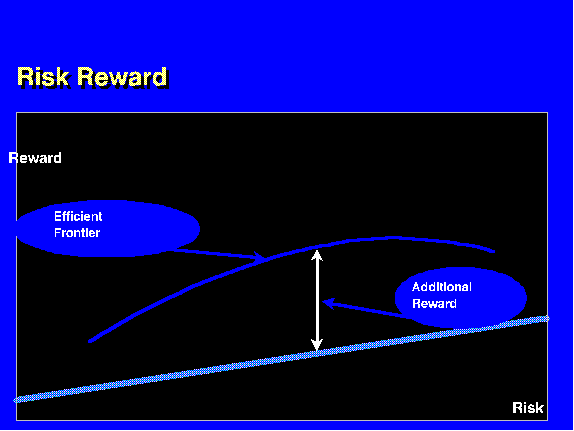
Рис. 4.4. Риск – вознаграждение
Оси: Риск — Вознаграждение
Граница эффективности располагается выше прямой риск-прибыль на величину дополнительного вознаграждения.

Каждая точка на границе эффективности предлагает инвестору максимальную доходность при заданном уровне риска. Но инвестор все еще имеет дело с бесконечным числом эффективных портфелей, и должен решить, какой риск ему принять. Ответ теоретика звучит так: «Выберите портфель на границе эффективности, в точке его касания к вашей кривой безразличия к риску!» Лично я думаю, что подобные ответы служат экономистам дурную славу. Неудивительно, что нас считают скучными и иногда немного странными! Далее я перечислю несколько способов, как инвесторам получить более жизненный ответ на этот вопрос. В то же время, если вы встретите инвестора, который знает, в каком месте его кривая безразличия касается границы эффективности, пожалуйста, попросите его связаться со мной. Думаю, я хотел бы встретиться с ним!

Процесс оптимизации в рамках СПТ позволяет инвестору подойти к инвестициям с двух точек зрения. Он может начать с принятия решения о том, какой риск он может комфортно выдерживать, а затем искать оптимальный уровень доходности в этой точке. Он мог бы рассмотреть задачу следующим образом: я хочу быть уверен на 95% (два стандартных отклонения), что мне не придется терпеть более, чем 10%-ное снижение стоимости портфеля в течение одного года. И советник поможет сформировать портфель, который имеет самый высокий возможный ожидаемый доход при заданном уровне риска. Либо инвестор может рассмотреть задачу так: я должен достичь доходности в 12%, и хочу сформировать портфель с минимально возможным уровнем риска.

Является ли СПТ бесплатным обедом? Нет, но СПТ — это невероятно мощный инструмент, позволяющий управлять рисками и строить портфели при заданных ограничениях. Марковиц, в большей степени чем кто-либо другой, вывел управление портфелем из тени на свет. Как мы увидим далее, СПТ имеет существенные ограничения, а также не приводит к избавлению от риска. Сегодня финансовый менеджмент все еще находится где-то между искусством и наукой. Но мы прошли долгий путь от алхимии. Инвесторы, желающие достичь чего-то, близкого к оптимальным инвестициям, не должны игнорировать СПТ. Проблема инвестиций имеет несколько измерений. Дни, когда вы могли бы решить проблему инвестиций, заведя дружественного брокера, который дал бы вам дружеский совет по выбору нескольких хороших акций, давно прошли. Если ваш консультант не использует СПТ, найдите другого советника.

В следующей главе мы рассмотрим, как далеко распространилась революция СПТ, увидим ее некоторые практические ограничения, и разберем два примера, которые демонстрируют конкретные преимущества для инвесторов.

Далее: Глава 5. Путешествие по границе эффективности
Оглавление

 

---

---

---

Комментариев: 8 »