Уильям Бернстайн: Бонус за ребалансировку – теория и практика

Уильям Дж. Бернстайн
Сентябрь 1996 г.
Efficient Frontier
Перевод для AssetAllocation.ru

Аннотация

Фактическая доходность ребалансируемого портфеля обычно превышает ожидаемую доходность, рассчитанную на основе взвешенной суммы ожидаемых доходностей компонентов. Выведена и протестирована формула для оценки этой избыточной доходности. Показано, что активы с высокой волатильностью и низкой корреляцией с остальной частью портфеля обеспечивают значительную избыточную доходность, или «бонус за ребалансировку».

Введение

Допустим, вы решили, что желаемый состав вашего портфеля состоит на 50% из акций индекса S&P 500 и на 50% из долгосрочных казначейских облигаций США. (Если вы так далеко зашли на этом сайте, то, вероятно, уже знаете, что это весьма нежелательное сочетание; просто оно служит хорошим примером). Поскольку эти два актива часто движутся в разных направлениях, портфель в конечном итоге будет отклоняться от желаемого соотношения 50/50. Если вы хотите сохранить состав 50/50, то часть более эффективного актива должна быть продана и обменена на аналогичную сумму актива с более низкими показателями. Это называется ребалансировкой портфеля. Понимание механики ребалансировки имеет фундаментальное значение для эффективного управления портфелем, и все же этой области уделялось на удивление мало теоретического внимания. Возникают три важных вопроса, касающихся ребалансировки:

1. Следует ли проводить ребалансировку через фиксированные регулярные промежутки времени («периодическая ребалансировка») или всякий раз, когда структура активов отклоняется на определенную величину («пороговая ребалансировка»)?
2. Если проводить ребалансировку периодически, то каков оптимальный интервал (например, ежемесячно, ежеквартально или ежегодно)?
3. Существует ли способ предсказать, какая дополнительная доходность будет получена в результате ребалансировки, и можно ли определить активы, которые принесут максимальную выгоду от ребалансировки?

Например, Марковиц (1) рассматривает доходность портфеля как взвешенную сумму доходностей отдельных компонентов, но такая формула работает только для портфелей без ребалансировки. Удивительно, что Марковиц рассматривал доходность портфеля как взвешенную сумму доходностей компонентов, поскольку именно он впервые выдвинул идею о том, что дисперсия портфеля, или риск, не является взвешенной суммой отдельных дисперсий компонентов. В работе «Выбор портфеля» (Portfolio Selection) он представил результат моделирования методом Монте-Карло, в котором фактическая доходность оказалась значительно выше ожидаемой доходности, полученной арифметически, однако, никак не прокомментировал расхождение.

Достаточно простого, хорошо известного примера: общая доходность акций за период 1926-94 гг. составила 10,19%, а доходность долгосрочных корпоративных облигаций за тот же период – 5,51%. (5) «Доходность Марковица» для сочетания этих двух активов в равных пропорциях равна среднему арифметическому или 7,85%. Ежегодная ребалансировка этого портфеля для поддержания соотношения 50/50 дает доходность 8,34%, принося бонус в размере 0,49% сверх доходности Марковица. Однако, если бы кто-то на самом деле 1 января 1926 г. вложил равные суммы денег в акции и облигации, никогда не ребалансировал портфель и не платил налоги, то долгосрочная доходность составила бы 9,17%. В этом случае портфель без ребалансировки имеет более высокую доходность, чем портфель с ребалансировкой. Это связано с тем, что за рассматриваемый 69-летний период доходность акций значительно превосходит доходность облигаций; и в последние 40 лет несбалансированный портфель более чем на 90% состоял бы из акций. Таким образом, более высокая доходность портфеля без ребалансировки достигается за счет гораздо более высокого риска, чем при ребалансировке.

Перольд и Шарп (2) указывают, что ребалансировка – это «вогнутая» стратегия. Страхование портфеля представляет собой противоположность ребалансировке и называется «выпуклой» стратегией. Они предполагают, что выпуклые стратегии страхования портфеля, а также стратегии «купи и держи» («плоские») приносят более высокую доходность на рынках с длительным восходящим (или нисходящим) трендом, а вогнутые стратегии ребалансировки приносят более высокую доходность на застоявшихся рынках. Если единственными двумя рассматриваемыми активами являются акции и облигации, и если доходность акций на длительном периоде времени всегда выше, чем доходность облигаций, то, очевидно, что стратегия «купи-и-держи», а также страхование портфеля, принесут доходность выше, чем при ребалансировке. Как уже было сказано, это произойдет за счет постепенного увеличения риска портфеля. Однако при рассмотрении глобальных портфелей акций дела обстоят совсем по-другому. На очень длительных временных горизонтах на большинстве национальных фондовых рынков обычно наблюдается относительно небольшая разница в доходности, и в таких условиях доминируют портфели с ребалансировкой. Например, если посмотреть на период 1970-94 гг., ребалансировка различных пар активов почти всегда обеспечивает доходность, превосходящую доходность портфелей без ребалансировки. Лишь в тех случаях, когда разница в долгосрочных доходностях между активами превышает 5%, портфели без ребалансировки обеспечивают более высокую доходность, да и то лишь за счет более высокого риска. (Исключениями, подтверждающими правило, являются очень высокая доходность японских акций и очень низкая доходность австралийских и итальянских акций.)

Следует обратить внимание на то, что превосходство ребалансировки в качестве долгосрочной стратегии относится только к национальным и региональным рынкам в целом, а не к различным отраслевым группам. В течение десятилетий целые отрасли промышленности часто приходят в упадок, в то время как другие сильно процветают. Ребалансировка фармацевтического и нефтяного сегментов S&P500 за последние три десятилетия была бы катастрофической стратегией. Хотя отдельные национальные рынки иногда исчезают в результате войн или национализаций, это происходит гораздо реже, чем продолжающееся изменение капитализации сегментов рынка, характерное для рыночной экономики.

Оценка бонуса за ребалансировку

Проведем небольшой мысленный эксперимент. Давайте представим портфель, состоящий из равных частей двух активов, A и B. Далее предположим, что каждый из них имеет доходность +30% или -10% с равной вероятностью, и что баланс портфеля будет возвращаться к соотношению 50/50 в конце каждого года. Долгосрочная доходность каждого актива составляет 8,1665% годовых, а её стандартное отклонение 20%. Если ежегодные доходности идеально коррелируют (т.е. r = 1), тогда сочетание A и B в равных пропорциях будет иметь тот же риск и ту же доходность, что и каждый отдельный актив, и диверсификация не принесет выигрыша в риске или доходности.
Теперь предположим, что между доходностями А и В существует нулевая корреляция. Это может быть символически представлено доходностями за четыре периода:

Случай 1

Актив:	Год 1	Год 2	Год 3	Год 4
100% A:	+30%	+30%	-10%	-10%
100% B:	+30%	-10%	+30%	-10%
50/50:	+30%	+10%	+10%	-10%

 

В этом примере годовая доходность составляет 9,0794%, а стандартное отклонение SD = 14,142%. Стандартное отклонение портфеля уменьшилось на коэффициент, равный квадратному корню из двух (а дисперсия уменьшилась вдвое), как и предсказывал Марковиц. Однако доходность на 0,9129% выше, чем доходность Марковица. Кроме того, эта избыточная доходность не была бы получена без ребалансировки. Таким образом, этот портфель имеет «бонус за ребалансировку» (далее именуемый «RB») в размере 0,9129%.

Если вместо этого доходности A и B находятся в идеальной обратной корреляции (r = -1), то можно видеть, что доходность портфеля каждый год будет составлять 10%, как и годовая доходность, а стандартное отклонение и дисперсия равны нулю. Таким образом, RB в этом чисто теоретическом примере составит 1,8355%, что чуть более чем вдвое превышает бонус в случае, когда r = 0.

Простое исследование показывает, что RB пропорционален выражению:

(1 – коэффициент корреляции)

Теперь предположим, что доходность актива А по-прежнему составляет +30% и –10%, но теперь доходность актива B может составлять либо +15%, либо +5%. В этом случае актив B имеет ожидаемую доходность 9,8863% (и стандартное отклонение SD = 10%, половину от актива А). Доходность Марковица для соотношения А и В 50%/50% составляет 9,0264% (среднее между 8,1665% и 9,8863% соответственно).

Для примера с некоррелированными активами r = 0:

Случай 2

Актив:	Год 1	Год 2	Год 3	Год 4
100% A:	+30%	+30%	-10%	-10%
100% B:	+15%	+5%	+15%	+5%
50/50:	+22,5%	+17,5%	+2,5%	-2,5%

 

Здесь годовая доходность составляет 9,5155%, что дает RB = 0,4891%, или примерно половину от примера с отсутствием корреляции в Случае 1. Дальнейшие эксперименты показывают, что бонус за ребалансировку любой комбинации двух активов приблизительно определяется выражением:

X₁ * X₂ * SD₁ * SD₂ * (1 – коэффициент корреляции)

где SD₁ – стандартное отклонение актива 1, X₁ – количество актива 1.

Делая следующий шаг в этом процессе, рассмотрим случай, когда актив с доходностью либо +30%, либо –10% смешивается с безрисковым активом, чья доходность всегда равна нулю. Доходность от сочетания этих двух активов в соотношении 50%/50% составит либо +15%, либо –5%. Доходность Марковица для этого сочетания составит 4,0833% (среднее значение между 8,1665% и 0%), но его фактическая доходность составляет 4,5227%, что дает RB = 0,4394%. Поскольку стандартное отклонение безрискового актива равно нулю, выражение, полученное выше, также будет равно нулю, поэтому уравнению требуется дополнительный член уравнения. Еще немного экспериментов показывают, что этот член может быть близко оценен выражением:

X₁ * X₂ * (SD₁ – SD₂)² / 2

Таким образом, постулируется, что «теоретический RB», RB₁₂, может быть выражен как:

RB_1,2 = X₁ * X₂ * {SD₁ * SD₂ * (1 – Corr_1,2) + (SD₁ – SD₂)² / 2}

Или, еще проще:

RB_1,2 = X₁ * X₂ * ((Var₁ / 2) + (Var₂ / 2) – Covar_1,2)

Иными словами, внутренний потенциал ребалансировки любой пары активов – это разница между их средней дисперсией и ковариацией. Приведенная выше формулировка была протестирована для сочетаний пар активов в соотношении 50%/50% для следующих активов: (5)

• Акции США (индекс S&P 500)
• Акции за пределами США (MCSI-EAFE)
• Акции малых компаний США (DFA USA small co. Portfolio)
• Акции трастов недвижимости REIT (индекс NAREIT)
• Акции Европы (MSCI-EAFE Europe)
• Акции Тихоокеанского региона (MSCI-EAFE Pacific)
• Акции развивающихся рынков (MSCI-EAFE Emerging Markets
• Акции малых компаний Великобритании (DFA UK small co. Portfolio)
• Акции малых компаний Японии (DFA Japanese small co. Portfolio)
• Акции малых компаний континентальной Европы (DFA Continental small co. portfolio)
• Драгоценные металлы (Morningstar fund index)
• Природные ресурсы (Morningstar fund index)
• Долгосрочные казначейские облигации (Lehman Long Term Government Index)
• Международные облигации (Morningstar fund index)
• Корпоративные однолетние облигации (DFA one year fixed fund)

Теоретический бонус за ребалансировку RB был рассчитан на основе стандартных отклонений SD и коэффициентов корреляции, полученных на основе квартальных данных за период с июля 1988 г. по декабрь 1994 г. Аналогичным образом «фактические» портфели ребалансировались ежеквартально. К каждой серии квартальных доходностей была применена линейная поправка, чтобы получить нулевую годовую доходность для каждого отдельного актива за весь исследуемый период. Таким образом, любая доходность, полученная от пары активов, должна быть обусловлена ребалансировкой.

Рис. 1: Фактический vs. Теоретический бонус за ребалансировку

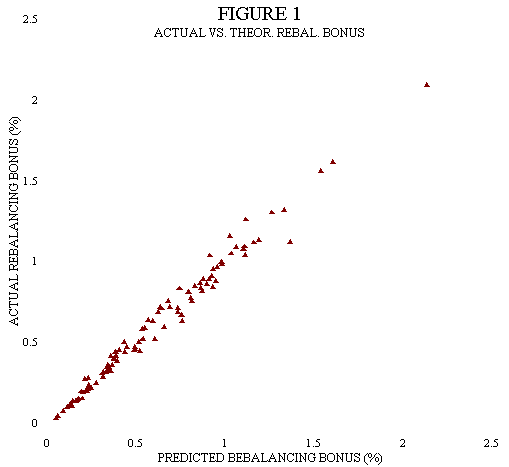
X – Рассчитанный бонус за ребалансировку
Y – Фактический бонус за ребалансировку

На Рис. 1 представлены 105 результирующих теоретических/фактических точек данных для каждой пары активов. Как видно, теоретические данные в высокой степени соответствуют фактическим данным с коэффициентом R² = 0,983 и стандартной ошибкой 0,052% от доходности.

Подводя итог вышесказанному: благотворное влияние слабо коррелированных активов на риск портфеля, несомненно ценимое с древнейших времен, были математически формализованы Марковицем всего сорок лет назад. Приведенная выше теоретическая модель и протестированные на истории портфели свидетельствуют о том, что для комбинаций пар активов, имеющих как низкую корреляцию, так и высокие риски, доступна значительная дополнительная доходность.

Модель оценки финансовых активов (capital asset pricing model — CAPM) утверждает, что «рискованная» часть портфеля должна быть «рыночным портфелем», взвешенным по капитализации, по всем инвестиционным рискованным активам мира. (3) Вышеизложенные соображения являются аргументом против взвешивания портфеля по капитализации, поскольку взвешивание по капитализации по определению отрицает необходимость ребалансировки. Активы и сектора, которые пострадали или были раздуты, обнаружат, что вес их капитализации соразмерно уменьшается или увеличивается. Рассмотрим индекс MSCI-EAFE /акции развитых рынков Европы, Австралии и Дальнего Востока — прим. переводчика/. В течение исследуемого периода, с июля 1988 г. по декабрь 1994 г., американские инвесторы, пассивно использовавшие этот индекс, наблюдали, как их доля в японских активах резко увеличивалась и уменьшалась. С другой стороны, инвестор, который хранил свои иностранные активы разделенными поровну между европейской и тихоокеанской сторонами этого индекса, получил бы избыточную доходность в размере 0,588% за исследуемый период, при умеренном сопутствующем снижении риска. Еще более ярким примером этого явления являются развивающиеся рынки. Латиноамериканская и дальневосточная составляющие индекса MSCI-EAFE Emerging Markets имеют очень высокие стандартные отклонения и слабую корреляцию. Приведенная выше модель предполагает, что инвестор, который активно ребалансирует эти два сектора, получит преимущество по меньшей мере в два-три процента по сравнению со своим коллегой, который инвестирует пассивно. Представляется весьма вероятным, что приверженность фиксированному процентному распределению между тонко разделенными секторами рынка дает значительные преимущества по сравнению с пассивным подходом к портфелю, взвешенному по рыночной капитализации.

Периодичность ребалансировки

Хотя необходимость ребалансировки портфеля для приведения в соответствие с инвестиционной политикой общепризнана, мало внимания уделялось его частоте. В редкой статье, посвященной этому вопросу, Арнотт и Ловелл (4) обнаружили, что в 1968-91 гг. соотношение акций и облигаций 50/50 привело к доходности 9,02% для ежегодной ребалансировки, 9,12% для ежеквартальной ребалансировки, и 9,16% для ежемесячной ребалансировки. Торговые издержки незначительно снижали выгоду от ребалансировки, но даже ежемесячная ребалансировка по-прежнему приносила пользу после учета транзакционных издержек. Они также обнаружили, что непериодическая «пороговая ребалансировка», когда отклонения долей портфеля превышали 1%, 2% и 5% избытка/недостатка, приводила к несколько меньшей прибыли. Они сделали следующее предположение: «В течение этого периода регулярная ежемесячная ребалансировка доминировала над менее активными подходами. Следует ли сделать вывод, что ежедневная ребалансировка еще лучше? Никто не может сказать, но это кажется правдоподобным».

Приведенная выше формулировка обеспечивает основу для дальнейшего исследования проблемы частоты ребалансировки. Можно рассчитать «теоретический бонус за ребалансировку» для каждого из различных периодов. Хорошо известно, что корреляции доходностей активов несколько меняются с течением времени. Менее известно, что индивидуальные доходности, стандартные отклонения доходностей и коэффициенты парной корреляции не одинаковы для различных интервалов выборки в пределах одного периода. Для одного и того же исторического периода стандартное отклонение доходностей одного и того же актива может различаться для более коротких и более длинных интервалов измерения. Еще большие различия могут наблюдаться в коэффициентах корреляции пар активов. Чтобы проиллюстрировать этот момент и заложить основу для дальнейшего обсуждения, я привел данные о стандартных отклонениях и корреляциях по пяти различным активам с месячной, квартальной и годовой доходностью в Таблице 1: малые компании Великобритании (UK SM), Японии (JAP SM), континентальной Европы (CONT SM) и США (US SM), а также развивающиеся рынки (MSCI-EM), опять же, за период с июля 1988 г. по декабрь 1994 г.. Эти конкретные активы выбраны из-за их низких взаимных корреляций и высоких стандартных отклонений доходностей.

Затем для полученных в результате 10 пар активов были рассчитаны «фактические» или «наблюдаемые» бонусы за ребалансировку RB для ежемесячной, ежеквартальной и ежегодной ребалансировки, и проведено сравнение с «теоретическими» или «прогнозируемыми» значениями. Данные представлены в Таблице 2.

Таблица 1

	SD (%)	CONT SM	JAP SM	MSCI-EM	US SM	UK SM
CONT SM	m: 14.54 q: 15.87 a: 19.86	m: 1.000 q: 1.000 a: 1.000
JAP SM	m: 32.29 q: 28.57 a: 24.63	m: .539 q: .483 a: .798	m: 1.000 q: 1.000 a: 1.000
MSCI-EM	m: 22.57 q: 27.06 a: 30.96	m: .154 q: .123 a: .634	m: .244 q: -.098 a: .653	m: 1.000 q: 1.000 a: 1.000
US SM	m: 14.71 q: 18.25 a: 19.50	m: .099 q: .007 a: -.154	m: .156 q: .217 a: .242	m: .379 q: .552 a: .590	m: 1.000 q: 1.000 a: 1.000
UK SM	m: 19.91 q: 17.79 a: 13.82	m: .620 q: .478 a: .251	m: .541 q: .478 a: .378	m: .305 q: .158 a: .614	m: .302 q: .309 a: .424	m: 1.000 q: 1.000 a: 1.000

 

(m = ежемесячные, q = ежеквартальные, a = ежегодные значения стандартных отклонений. Все стандартные отклонения SD рассчитаны в годовом исчислении, вдвое выше квартальных SD и в 3,4641 раза выше месячных SD)

Таблица 2

Пара активов	Ежемесячный RB факт / прогноз	Квартальный RB факт / прогноз	Ежегодный RB факт / прогноз
CONT SM/JAP SM	0.911/0.871	0.818/0.787	0.345/0.275
CONT SM/MSCI-EM	0.788/0.778	1.099/1.102	0.941/0.717
CONT SM/US SM	0.484/0.482	0.694/0.762	1.171/1.118
CONT SM/UK SM	0.311/0.311	0.412/0.369	0.529/0.551
JAP SM/MSCI-EM	1.455/1.469	2.099/2.125	0.681/0.712
JAP SM/US SM	1.347/1.388	1.124/1.153	0.929/0.943
JAP SM/UK SM	0.917/0.930	0.885/0.940	0.710/0.678
MSCI-EM/US SM	0.591/0.592	0.600/0.650	0.705/0.783
MSCI-EM/UK SM	0.787/0.790	1.267/1.109	0.987/0.779
UK SM/US SM	0.541/0.545	0.644/0.651	0.477/0.428

 

Эти данные позволяют сделать три основных вывода:

1. Ни один период ребалансировки не является доминирующим. Ежемесячная ребалансировка была наилучшей в трех случаях, ежеквартальная в четырех и ежегодная в трех.
2. Теоретический RB был высоко предсказуемым во всех случаях, когда при разных интервалах были получены существенно отличающиеся бонусы за ребалансировку. Только в трех случаях были допущены незначительные (<0,05%) ошибки ранжирования. Кроме того, в случаях, когда использование определенного периода ребалансировки приносит значительное преимущество, сложные расчеты не требуются. Например, обращаясь к Таблице 2, можно увидеть, что для пары Япония/Развивающиеся рынки, ежеквартальная ребалансировка явно превосходит ежемесячную или ежегодную. Это хорошо отражается в прогнозируемых значениях, и из Таблицы 1 видно, что это связано, прежде всего, с тем, что квартальный коэффициент корреляции значительно ниже месячных или годовых значений.
3. Те, кто полагается на процедуры оптимизации, должны быть осведомлены об интервале выборки, который использовался для расчета стандартного отклонения и корреляций. Результаты оптимизации могут сильно различаться для данных, полученных в результате ежемесячной, ежеквартальной и ежегодной выборки за один и тот же исторический период.

Очевидно, что реальные портфели намного сложнее, чем портфели из двух активов. Представляется разумным предположить, что по аналогии с формулой Марковица для дисперсии портфеля формулу для RB портфеля можно представить следующим образом:

½ * (SUM _i=1..n) * (SUM _j=1..n) * RB_ij

(Каждый член, для которого i=j, будет равен нулю)

Применение этой формулы к равному сочетанию (по 20% каждого) из пяти активов, использованных выше, дает наблюдаемый/прогнозируемый RB = 1,205/1,118% для ежегодных ребалансировок, RB = 1,542/1,556% для ежеквартальных и 1,304/1,301% для ежемесячных. В годовом исчислении стандартные отклонения портфеля SD составляют 16,80% для ежегодных ребалансировок, 13,65% для ежеквартальных и 14,55% для ежемесячных – тот же рейтинг предпочтений, что и для RB. Это не должно удивлять, поскольку ковариация пары активов является доминирующим компонентом как для RB портфеля, так и для дисперсии портфеля для портфелей, в которых более двух составляющих.

Необходима дальнейшая работа, чтобы оценить ценность этой формулы для оценки выгоды от ребалансировки более сложных портфелей. Может оказаться, что сложная взаимосвязь между парными корреляциями и стандартными отклонениями отдельных активов, измеренными за более короткие или более длительные периоды времени, не будут достаточно стабильной.

Драгоценные металлы – особый случай

Портфельные характеристики драгоценных металлов уникальны: очень низкая долгосрочная доходность, очень высокая дисперсия доходности и почти нулевая корреляция с большинством других классов активов. Одним из основных объяснений такого поведения является то, что большая часть рисков этого класса активов является несистемной из-за его низкой корреляции с другими активами – другими словами, его можно использовать для диверсификации. Приведенное выше обсуждение дает другой взгляд на этот парадокс. Изучение теоретической формулы ребалансировки показывает, что добавление небольшого количества актива с высокой дисперсией и нулевой корреляцией к портфелю с гораздо меньшей дисперсией увеличивает его расчетную доходность примерно на половину его дисперсии. Другими словами, поскольку дисперсия типичного портфеля акций драгоценных металлов составляет около 0,1, его расчетная доходность (IRR) в ребалансируемом портфеле окажется примерно на 5% выше, чем его долгосрочная самостоятельная доходность. Это именно то, что наблюдает инвестор, который периодически ребалансирует долю драгоценных металлов в своем портфеле в виде фиксированной пропорции; значительная часть доходности портфеля приходится на ребалансировку как таковую. Таким образом, не только системный риск драгоценных металлов намного ниже, чем их самостоятельный риск, но и доходность ребалансируемого портфеля намного выше, чем наблюдаемая долгосрочная доходность.

Выводы:

1. Ожидаемая доходность ребалансируемого портфеля не может быть точно представлена простым арифметическим взвешиванием доходности отдельных активов. Это особенно верно в отношении активов, которые имеют высокие стандартные отклонения и слабую корреляцию. Это может иметь некоторое значение для тех, кто использует технологию оптимизации, зависящую от определения ожидаемой доходности. Стандартные методы MVO недооценивают преимущества активов с высокой дисперсией / низкой корреляцией.
2. Взвешивание по капитализации, предлагаемое моделью CAPM, по-видимому, не является максимально эффективным.
3. Представлена формула, которая точно предсказывает выгоду от ребалансировки. Входными данными для этого уравнения являются состав портфеля, стандартные отклонения/дисперсии отдельных активов и корреляции/ковариации пар активов. Поскольку эти параметры изменяются в зависимости от интервала выборки, возможно, удастся использовать эту формулу для прогнозирования оптимальной частоты ребалансировки. Кроме того, результаты представленного анализа свидетельствуют о том, что более короткие периоды ребалансировки не всегда бывают оптимальны.
4. Оптимизаторы должны понимать, что интервал выборки существенно влияет как на входные, так и на выходные данные, и что они оптимизируют только стандартные отклонения (или другие меры риска, таких как полудисперсия) в течение заданного интервала выборки.

Ссылки:

1. Harry M. Markowitz, Portfolio Selection: Efficient Diversification of Investments, 2nd ed. (Cambridge, Massachusetts: Basil Blackwell Ltd., 1991), 67.
2. Andre F. Perold and William F. Sharpe, «Dynamic Strategies for Asset Allocation», Financial Analysts Journal (January/February 1988):16-27.
3. Roger G. Ibbotson and Gary P. Brinson, Global Investing: the Professional’s Guide to the World Capital Markets (New York: McGraw Hill Inc., 1992), 43-44.
4. Robert D. Arnott and Robert M. Lovell, «Rebalancing: Why? When? How Often?», The Journal of Investing, no. 1 (Spring 1993): 5.
5. US stock and bond returns from Stocks, Bonds, Bills and Inflation 1995 Yearbook, Ibbotson Associates, Inc., Chicago. The 1988-94 quarterly returns data were obtained from Principia for closed and open end funds from Morningstar Associates, Chicago.

 

 

---

---

---

Комментариев нет »