Гарри Марковиц: Выбор портфеля

Гарри Марковиц
The Journal of Finance, том 7, №1, стр. 77–91
Март 1952 г.

Процесс формирования портфеля (ценных бумаг) можно разделить на два этапа. Первый этап заключается в анализе исторических данных и формировании ожиданий относительно будущей доходности доступных для инвестирования инструментов. Второй этап в качестве отправной точки опирается на ожидания о будущей доходности, а целью имеет окончательный выбор портфеля. В данной работе рассматривается именно второй этап.

В первую очередь мы обсудим принцип формирования портфеля, в соответствии с которым инвестор стремится достичь наибольшего ожидаемого будущего приведенного дохода. Мы придем к тому, что этот принцип нужно отвергнуть, как в качестве гипотезы, объясняющей фактическое поведение инвесторов, так и в качестве рекомендации к действию. Далее мы проанализируем другое правило выбора портфеля, в соответствии с которым инвестор рассматривает (должен рассматривать) увеличение дохода как желательный, а увеличение дисперсии дохода как нежелательный результат инвестирования. Имеется много данных, подтверждающих применимость этого правила и как руководящего принципа, и как гипотезы для объяснения поведения участников рынка. Мы геометрически изобразим отношения между оценкой инвестором рыночных условий и выбором портфеля, основываясь на правиле «ожидаемая доходность – дисперсия доходности» (так называемое правило «Е-V»).

* * *Итак, вначале мы рассмотрим правило, описывающее выбор портфеля, согласно которому инвестор стремится (должен стремиться) получить наибольшую приведенную доходность. Поскольку будущее не является однозначно определенным, необходимо использовать «ожидаемую» окупаемость, которую мы дисконтируем, приводя к долларам сегодняшнего дня. На практике могут применяться различные версии этого правила. Согласно Дж. Р. Хиксу, при вычислении ожидаемой доходности может быть использован определенный допуск на риск, также различный уровень риска можно учитывать, используя разные значения ставки дисконтирования.

Автор утверждает, что гипотеза, или рекомендация, согласно которой единственным критерием является увеличение дисконтированной доходности, должна быть отвергнута. Основная причина этого заключается в том, что если мы не примем во внимание неэффективность рынка, из вышеупомянутого правила не следует предпочтение диверсифицированных портфелей перед недиверсифицированными. В то же время, как несложно заметить, диверсификация является важным фактором будущей доходности портфеля. Правило поведения, из которого не следует превосходство диверсифицированных портфелей над недиверсифицированными, не может быть принято к рассмотрению как гипотеза и как рекомендация.

Из вышеупомянутого правила не следует необходимость диверсификации при любом способе оценки будущих доходов, любом выборе (одинаковых или различных) ставок дисконтирования, а также динамики ставок дисконтирования во времени. Рекомендуемым поведением инвестора, исходя из гипотезы, является вложение всех имеющихся в его распоряжении средств в одну ценную бумагу с наибольшей приведенной доходностью. Если же имеется две и более ценных бумаги с одинаковой приведенной доходностью, инвестору будет безразлично, в какую из них или в какую их комбинацию вкладывать.

Мы можем представить аналитическое обоснование данного утверждения. Предположим, что имеется N ценных бумаг. Обозначим
r_it – ожидаемый доход в момент времени t на каждый доллар, инвестированный в ценную бумагу i
d_it – фактор дисконтирования, применяемый к доходу, принесенному i-той ценной бумагой в момент t
X_i – Доля средств, инвестированных в ценную бумагу i

В данной работе мы исключим из рассмотрения случай коротких продаж, поэтому X_i ≥ 0 при любом i. Таким образом, приведенный ожидаемый доход портфеля ценных бумаг может быть описан формулой

	∞	N		N			∞
R=	∑	∑	ditritXi=	∑	Xi	(	∑	ditrit	)
	t=1	i=1		i=1			t=1

Обозначим приведенный доход i-ой ценной бумаги R_i = ∑_td_itr_it. Таким образом, имеем R=∑_iX_iR_i, где R_i не зависит от X_i. Так как X_i ≥ 0 для всех i, и ∑_iX_i=1, то R представляет собой линейную комбинацию R_i с неотрицательными весовыми коэффициентами X_i. Для достижения максимального значения R нам необходимо положить X_i=1 для i с наибольшим R_i и X_j=0 для остальных j≠i.

Если равное максимальное значение принимает несколько R_i, а именно R_ia, где a = 1, … K, то любое распределение средств, при котором ∑_aX_ia =1 ведет к максимальным значениям R. Ни при каких значениях исходных данных диверсифицированный портфель не является предпочтительнее недиверсифицированного, если принять такой подход к оптимизации.

Далее рассмотрим статическую модель, то есть вместо рассмотрения временных рядов дохода от i-той ценной бумаги вида (r_i1, r_i2, … r_it, …), будем рассматривать «постоянный поток доходов» (r_i) от i–ой ценной бумаги. Поток доходов от портфеля в целом можно вычислить как сумму R=∑_iX_ir_i. Так же, как и в динамическом случае, инвестор, стремящийся увеличить ожидаемый доход от инвестиционного портфеля, поместит все доступные средства в ценную бумагу с максимальной ожидаемой доходностью.

* * *Существует иное правило распределения активов, которое действительно приводит к тому, что инвестор стремится и к диверсификации и к увеличению ожидаемого дохода. Правило гласит, что инвестор распределяет (должен распределять) средства между всеми бумагами, дающими наибольший ожидаемый доход. Утверждается, что в соответствии с законом больших чисел, фактический доход от инвестиций в этом случае будет приблизительно равен ожидаемому. Это правило является частным случаем правила «ожидаемая доходность – дисперсия доходности» (обсуждается ниже). Метод предполагает, что существует портфель, дающий одновременно наибольший ожидаемый доход и минимальную дисперсию. Данный портфель и рекомендуется инвестору.

Однако, предположение, что закон больших чисел применим к портфелю ценных бумаг, не может быть принято для всех случаев, поскольку доходы от ценных бумаг не являются независимыми случайными величинами. А значит, диверсификация не способна устранить всю неопределенность. Портфель с наибольшим ожидаемым доходом, совсем не обязательно является портфелем, с минимальной дисперсией. Существует некая «цена» низкой дисперсии: для снижения дисперсии портфеля инвестор, переходя к некоторому другому портфелю, «жертвует» высокой ожидаемой доходностью.

* * *Как видно из вышесказанного, правило ожидаемого или оцененного дохода является неудовлетворительным. Теперь рассмотрим правило «ожидаемой доходности – дисперсии доходности» (правило «E-V»). В первую очередь мы представим ряд основных понятий математической статистики. Затем, будут показаны следствия правила «E-V». После этого мы обсудим применимость данного метода.

В рамках данной работы, мы стараемся избегать сложных математических выкладок и доказательств. Как следствие, описываемая модель становится менее общей и строгой. Основное ограничение состоит в том, что мы, во-первых, не рассматриваем случай n ценных бумаг. Вместо этого мы анализируем геометрически случаи трех и четырех ценных бумаг. А во-вторых, мы рассматриваем случай постоянных (во времени) вероятностных распределений доходности. В более общем случае вероятностное распределение доходов от ценных бумаг должно меняться со временем. Автор намерен в будущем разработать математический аппарат, который позволит рассматривать данную задачу в общем виде.

Нам потребуются следующие основные понятия математической статистики. Пусть Y – случайная величина. Это значит, что ее значение определяется в ходе некоторого процесса, исход которого не определен заранее. Для облегчения представления, предположим, что Y может принимать конечное число значений y₁, y₁, … y_N. Обозначим вероятность того, что Y=y₁, как p₁, того что Y=y₂, как p₂ и т. д. Математическое ожидание Y определяется по формуле:

E = p₁ y₁ + p₂ y₂ + … p_N y_NДисперсия Y определяется следующим образом:

V = p₁ (y₁ − E)² + p₂ (y₂ − E)² + … p_N (y_N − E)²V (дисперсия случайной величины Y) равна математическому ожиданию квадрата отклонения Y от его математического ожидания. V наиболее часто используется в качестве меры «разброса» величины вокруг ее среднего значения. Другими мерами разброса, связанными с V являются среднеквадратическое отклонение σ=√V и коэффициент вариации σ/E.

Предположим, что у нас есть несколько случайных величин R₁, … R_n. Их линейная комбинация (взвешенная сумма, сумма с коэффициентами),

R = a₁R₁ + a₂R₂ + … + a_nR_nтакже является случайной величиной (В качестве примера пусть R₁ – число, выпавшее на одном игральном кубике, R₂ – соответственно, на втором, а R – сумма этих чисел. В данном случае n=2, a₁=a₂=1).

В дальнейшем нам пригодится связь математического ожидания и дисперсии линейной комбинации (R) с распределением R₁, … R_n. Данные соотношения будут приведены ниже без доказательства, читатель, желающий ознакомиться с их доказательством, может обратиться к любому вводному курсу математической статистики.

Математическое ожидание линейной комбинации является линейной комбинацией математических ожиданий с теми же коэффициентами:

ER = a₁ER₁ + a₂ER₂ + … + a_nER_nОпределение дисперсии линейной комбинации выражается несколько сложнее. Для ее представления, нам потребуется понятие «ковариация». Ковариация случайных величин R₁ и R₂ определяется формулой

σ₁₂ = E{ (R₁ − ER₁)(R₂ − ER₂) },т. е. математическое ожидание произведения отклонения R₁ от его математического ожидания и отклонения R₂ от его математического ожидания. Аналогично ковариация между R_i и R_j определяется по формуле

σ_ij = E{ (R_i − ER_i)(R_j − ER_j) },σ_ij может быть выражена через коэффициент корреляции (ρ_ij). Ковариация между R_i и R_i равна произведению коэффициента корреляции R_i и R_i и среднеквадратических отклонений R_i и R_j:

σ_ij = ρ_ijσ_iσ_jДисперсия линейной комбинации определяется формулой

	N			N	N
V(R)=	∑	ai2V(Ri)	+ 2	∑	∑	aiajσij
	i=1			i=1	j>i

Если воспользоваться тем, что дисперсия R_i равна σ_ii, тогда получим:

	N	N
V(R)=	∑	∑	aiajσij
	i=1	j=1

здесь R_i – доходность i-той ценной бумаги,
µ_i – математическое ожидание R_i,
σ_ij – ковариация между R_i и R_i (таким образом, σ_ii является дисперсией R_i),
X_i – доля средств инвестора, размещенных в i-той ценной бумаге.

Доходность портфеля в целом, следовательно, будет составлять R=∑_iX_iR_i, при этом R_i (и соответственно R) рассматриваются как случайные величины. X_i не являются случайными величинами, они выбираются инвестором. Поскольку X_i представляют собой веса ценных бумаг в портфеле, то их сумма должна быть равна единице: ∑_iX_i = 1.

В рамках данного анализа, отрицательные значения X_i (т. е. короткие продажи) будут исключены из рассмотрения, следовательно, X_i ≥ 0 при любом i.
Доход портфеля в целом представляет собой линейную комбинацию случайных величин, в которой инвестор имеет возможность выбирать вес каждой из них. Исходя из изложенного выше, очевидно, что математическое ожидание Е доходности портфеля в целом будет определяться формулой

E = ∑_iX_iμ_iа дисперсия

V = ∑_i∑_jσ_ijX_iX_jПри заданных величинах (µ_i, σ_ij) инвестор имеет возможность выбрать одну из множества комбинаций E и V, меняя веса ценных бумаг портфеля (X₁, X₂, … X_N). Пусть множество доступных комбинаций (E, V) описывается фигурой, изображенной на рисунке 1.

Рисунок 1Правило «E-V» гласит, что инвестор стремится выбрать портфель, соответствующий комбинациям с минимальным V для заданного и больших значений E и с максимальным E для заданного и меньших значений V. Мы будем называть их «эффективные портфели». Можно указать методы, помогающие вычислять форму множества эффективных портфелей и эффективных комбинаций (E, V) для данных µ_i и σ_ij. В этой работе такие методы в деталях не рассматриваются. Вместо этого, мы представим геометрическую иллюстрацию поверхностей, дающих эффективные (в указанном выше смысле) комбинации ценных бумаг для случая, когда N невелико.

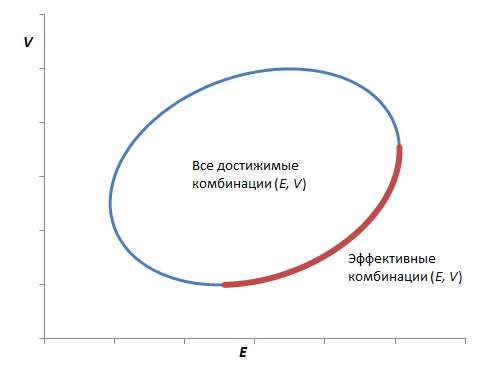
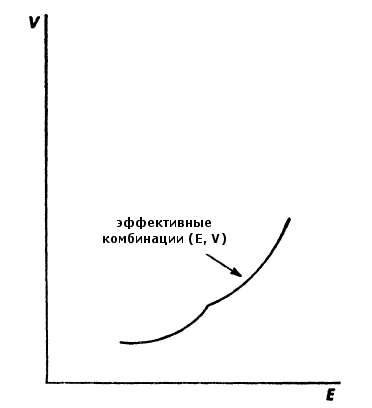
Метод определения поверхностей, дающих эффективные комбинации ценных бумаг, действительно может быть использован на практике. Предположим, что существует способ вывести достаточно качественные оценки (µ_i, σ_ij) на основе комбинации статистических методов и экспертных суждений. Полученные значения могут быть использованы для вычисления достижимых эффективных комбинаций (E, V). Далее, инвестор, обладающий информацией о достижимых комбинациях (E, V), может указать из них наиболее предпочтительную для себя. После этого несложно найти портфель, дающий указанную комбинацию.

Применение методов поиска множества эффективных портфелей (границы эффективности) предполагает выполнение как минимум двух условий. Во-первых, инвестор должен принять в качестве руководства к действию правило «E-V». Во-вторых, мы должны иметь возможность получить достаточно достоверную оценку µ_i и σ_ij. К рассмотрению этих моментов вернемся позже.

Рассмотрим вариант, при котором портфель формируется из трех ценных бумаг. В этом случае модель приводится к виду

		3
(1)	E=	∑	Xiµi
		i=1

		3	3
(2)	V=	∑	∑	XiXjσij
		i=1	j=1

	3
(3)	∑	Xi=1
	i=1

(4) X_i ≥ 0 для i = 1, 2, 3

Из (3) получаем

(3′) X₃ = 1 − X₁ − X₂

Далее, подставляя (3′) в уравнения (1) и (2), получим E и V, выраженные через X₁ и X₂.

Точные формулы в данной ситуации не столь важны, однако приведем их здесь для полноты изложения:

(1′) E = μ₃ + X₁ (μ₁ − μ₃) + X₂ (μ₂ − μ₃)

(2′) V = X₁² (σ₁₁ − 2σ₁₃ + σ₃₃) + X₂²(σ₂₂ − 2σ₂₃ + σ₃₃) + 2X₁X₂(σ₁₂ − σ₁₃ − σ₂₃ + σ₃₃) + 2X₁(σ₁₃ − σ₃₃) + 2X₂(σ₂₃ − σ₃₃) + σ₃₃

В дальнейшем будем использовать просто условия

(a) E = E(X₁, X₂)

(b) V = V(X₁, X₂)

(с) X₁ ≥ 0; X₂ ≥ 0; 1 − X₁ − X₂ ≥ 0.

К выражениям (а), (b), (c) можно применять инструменты геометрии на плоскости.

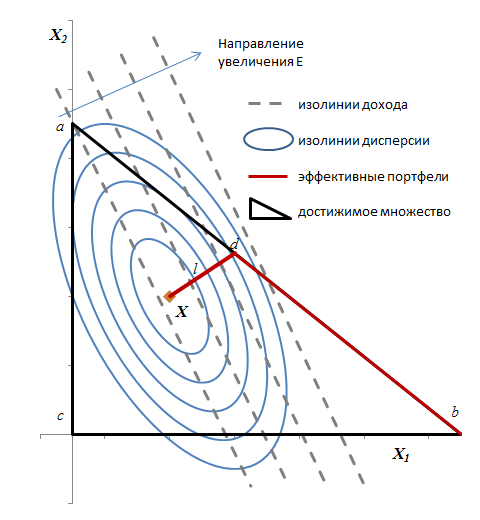
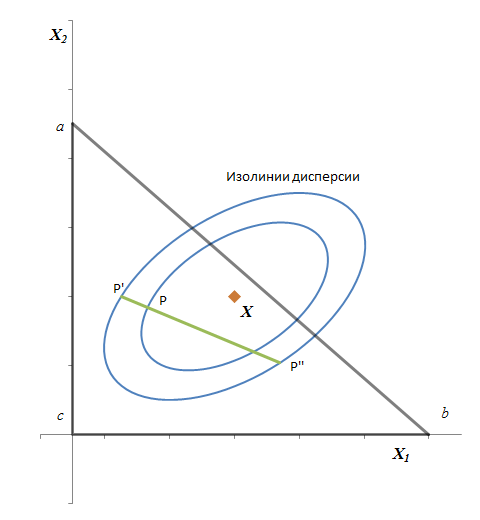
Достижимое множество портфелей представлено точками, удовлетворяющими условиям (с) и (3′) (или эквивалентным им (3) и (4)). Возможные комбинации X₁ и X₂ заполняют собой треугольник abc на рисунке 2. Любая точка слева от оси X₂ недостижима, поскольку нарушает условие X₁ ≥ 0. Любая точка ниже оси X₁ также недостижима, поскольку нарушает условие X₂ ≥ 0. Любая точка над линией 1 – X₁ – X₂ = 0 недостижима, т. к. для таких точек нарушается условие, X₃ = 1 – X₁ – X₂ ≥ 0

Введем понятие изолинии ожидаемого дохода, состоящей из всех точек (портфелей) с заданным ожидаемым доходом. Также, введем понятие изолинии дисперсии, состоящей из всех точек (портфелей) с заданной дисперсией дохода. Формулы для E и V позволяет определить формы изолиний ожидаемого дохода и дисперсии. Как правило, изолинии ожидаемого дохода это система параллельных прямых, изолинии дисперсии – система концентрических эллипсов (см. рисунок 2). Действительно, если µ₂ ≠ µ₃, уравнение (1′) может быть записано в форме X₂ = a + bX₁. А именно из (1) следует, что

X₂ =(E−µ₃) / (µ₂−µ₃) — (µ₁−µ₃) / (µ₂−µ₃)

Таким образом, угловой коэффициент изолинии ожидаемого дохода, связанной с E = E₀ равен

— (µ₁−µ₃) / (µ₂−µ₃)

а ее свободный член

(µ₂−µ₃) / (E₀−µ₃)

Придавая разные значения E, мы придем к различным свободным членам, но угловой коэффициент, а значит и наклон изолинии ожидаемого дохода, останется неизменным. Это доказывает справедливость утверждения о том, что изолинии ожидаемого дохода – система параллельных прямых.

Также, применяя несколько менее элементарные инструменты аналитической геометрии, можно доказать, что изолинии дисперсии – система концентрических эллипсов. Центром системы будет точка, в которой значение V будет наименьшим. Назовем эту точку X. Ожидаемый доход и дисперсию в этой точке будем называть E и V. Дисперсия будет увеличиваться при удалении от X. Точнее, если некая изолиния дисперсии C₁ лежит ближе к X, нежели C₂, то C₁ будет соответствовать меньшей дисперсии, нежели C₂.

Используя данный геометрический аппарат, перейдем к поиску границы эффективности.

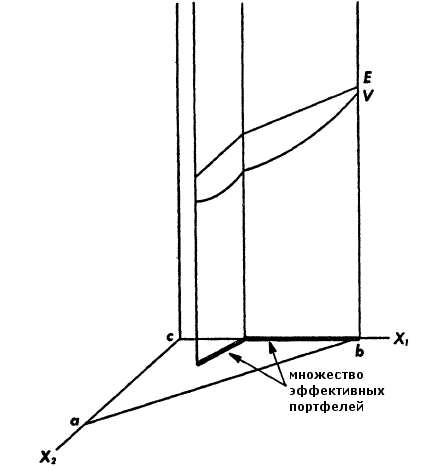
Точка X – центр системы эллипсов – изолиний дисперсии, может лежать как в пределах достижимого множества, так и вне его. На рисунке 2 изображена ситуация, при которой X лежит в пределах достижимого множества. В такой ситуации X принадлежит множеству эффективных портфелей. Действительно, не существует портфеля, имеющего меньшее V (при столь же большом E) или большее E (при столь же малом V), поскольку не существует вообще ни одной точки с меньшим V. Ни одна точка (портфель) с ожидаемым доходом E меньшим, чем E не может быть эффективной. Таким образом, E > E, и V > V.

Рассмотрим все точки с данным ожидаемым доходом E, т. е. все точки на изолинии ожидаемого дохода, соответствующей доходу E. Точка изолинии ожидаемого дохода, в которой V принимает наименьшее значение, является точкой, в которой изолиния ожидаемого дохода касается изолинии дисперсии. Обозначим эту точку X(E) При изменениях E, X(E) будет двигаться вдоль некоторой линии. Алгебраические вычисления, опускаемые в рамках этой работы, показывают, что данная линия является прямой. Назовем ее критической линией l.
Она проходит через точку X, в которой V принимает наименьшее значение среди всех точек, отвечающих условию E(X₁, X₂) = E. При движении по l от X в любом направлении V будет увеличиваться.

Рисунок 2Отрезок критической линии от X до точки пересечения с границей достижимого множества, является частью границы эффективности. Вторая часть границы эффективности (в описываемом случае) отрезок прямой ab от d до b; где b – точка с максимальным достижимым значением E.

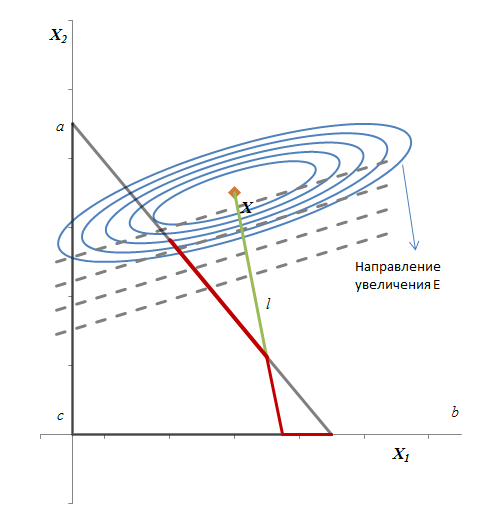
На рисунке 3 точка X лежит за пределами достижимой зоны, критическая линия проходит через достижимую зону. Линия эффективности начинается в достижимой точке с наименьшей дисперсией (в данном случае, она находится на линии ab). Линия проводится в направлении точки b до пересечения с критической линией, далее вдоль критической линии до пересечения с другой границей достижимого множества, и, наконец, вдоль другой границы к точке b.

Рисунок 3Читатель может пожелать изучить и другие варианты.

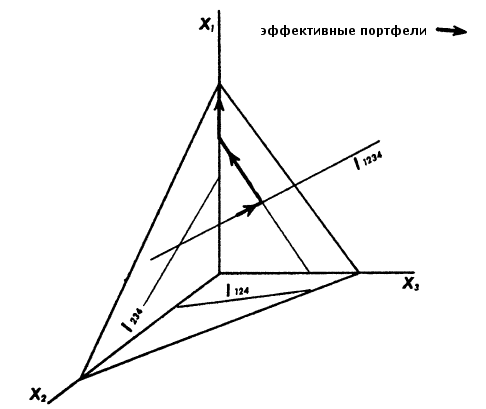
1. X лежит вне достижимого множества и критическая линия не проходит через него. В такой ситуации существует ценная бумага, которая не входит ни в один эффективный портфель.
2. Две ценные бумаги имеют одинаковые µ_i. В такой ситуации, изолинии ожидаемого дохода параллельны границе треугольника abc. Это может привести к тому, что эффективным портфелем с наибольшим E станет диверсифицированный портфель.
3. Существует только один эффективный портфель.

* * *Эффективное множество для варианта с четырьмя ценными бумагами (также как для вариантов с тремя или N > 4 ценными бумагами) представляет собой набор замкнутых линий. На одном конце эффективного множества лежит точка наименьшей дисперсии, на другом – точка максимального ожидаемого дохода (см. рис. 4).

Рисунок 4После рассмотрения множества эффективных портфелей, понять характер множества эффективных комбинаций (E, V) несложно. Для варианта с тремя ценными бумагами, график E будет представлять собой плоскость, а V – параболоид:

E = a₀ + a₁X₁ + a₂X₂

 V = b₀ + b₁X₁ + b₂X₂ + b₁₂X₁X₂ + b₁₁X₁² + b₂₂X₂²

 

Рисунок 5Как показано на рисунке 5, часть графика E, построенного над множеством эффективных портфелей представляет собой ломаную. В свою очередь, часть графика V (являющегося параболоидом) над множеством эффективных портфелей представляет собой набор последовательно соединенных сегментов параболы. При этом, если изобразить эффективные портфели на плоскости переменных (E, V), мы вновь получим набор соединенных сегментов параболы (см. рис. 6). Результат справедлив для любого набора ценных бумаг.

Рисунок 6По множеству причин рекомендуется использование правила «E-V» как в качестве гипотезы для объяснения разумного инвестиционного поведения, так и в качестве руководства к действию. Следует впрочем отметить, что правило лучше подходит именно для «инвестиционного», а не «спекулятивного» поведения.

* * *Ранее мы отвергли правило ожидаемой доходности, так как из него не следовало превосходство диверсификации. Правило «Е-V», напротив, приводит к необходимости диверсификации для широкого диапазона исходных µ_i и σ_ij. Из этого не следует, однако, что правило «E-V» никогда не установит в качестве рекомендации недиверсифицированный портфель. Вполне возможна ситуация, при которой некая ценная бумага будет иметь настолько большую доходность и настолько низкую дисперсию (относительно остальных ценных бумаг), что недиверсифицированный портфель, состоящий только из этой бумаги, будет обладать наибольшим E и наименьшим V из возможных.
Однако, в существенной и вероятно репрезентативной выборке µ_i и σ_ij, практически все эффективные портфели при использовании правила «Е-V» окажутся диверсифицированными.

Гипотеза «E-V» подразумевает не просто диверсификацию, а «правильную» диверсификацию по «правильной» причине. Достаточность диверсификации не определяется одним лишь количеством ценных бумаг различных компаний. Так, портфель с 60 ценными бумагами различных железнодорожных компаний, не может считаться столь же качественно диверсифицированным, как портфель того же размера, включающий в себя ценные бумаги железнодорожных, энергосбытовых, горнодобывающих, производственных и прочих компаний. Причина этого заключается в том, что, как правило, одновременное возникновение затруднений у нескольких компаний более вероятно, если эти компании принадлежат одной отрасли.

Таким образом, для уменьшения дисперсии портфеля недостаточно просто вкладывать деньги в большое количество ценных бумаг. Одновременно следует избегать размещения средств в ценных бумагах c высокой корреляцией финансовых результатов. Диверсификацию следует проводить и между отраслями, поскольку поведение ценных бумаг компаний разных отраслей (особенно отраслей, успех которых зависит от различных макроэкономических тенденций) обладают меньшей корреляцией, нежели компаний из одной отрасли.

Термины «доходность» и «риск» упоминаются в научных работах на тему финансов достаточно часто. Как правило, под «доходностью» подразумевают «ожидаемый доход», а «риск» выражен количественно через «дисперсию доходности».

Дисперсия – распространенная мера «разброса» величины вокруг ее среднего значения. Если же вместо дисперсии инвестор решит применить среднеквадратическое отклонение σ=√V или коэффициент вариации σ/E, то полученный результат по-прежнему будет находиться среди введенного нами множества эффективных портфелей.

* * *Теперь предположим, что инвестор распределяет средства между двумя портфелями (т. е. вкладывает часть денег в один портфель, и часть – в другой. Примером диверсификации между портфелями служит покупка акций двух инвестиционных фондов.) Если два исходных портфеля обладают одинаковой дисперсией, то, как правило, дисперсия полученного составного портфеля будет меньше, нежели дисперсия каждого из исходных.

Рисунок 7Данная ситуация показана на рисунке 7. Чтобы объяснить рисунок 7, отметим, что портфель (P), созданный на основе двух портфелей P′=(X′₁,X′₂) и P″=(X″₁,X″₂) имеет вид

P = λP′ + (1 − λ)P″ = ( λX′₁ + (1 − λ)X″₁, λX′₂ + (1 − λ)X″₂ )точка P лежит на прямой, соединяющей P′ и P″.

Как уже отмечалось, правило «E-V» более применимо для инвестиционного, а не спекулятивного поведения. Третий момент M₃ (для случайной величины R, принимающей конечное число значений r₁, … r_N с вероятностями p₁, … p_N по определению M₃ = ∑_ip_i(r_i − E)³) распределения вероятности доходов от портфеля может быть связан со склонностью к риску.

К примеру, стремясь достичь максимальной полезности U, зависящей от E и V (U=U(E, V), ∂U/∂E > 0, ∂U/∂V < 0), инвестор никогда не сделает справедливую (ставку, при которой выигранная сумма кратна вероятности выигрыша) ставку.

Однако, при условии U=U(E, V, M₃) и ∂U/∂E > 0, ∂U/∂V < 0 и ∂U/∂M₃ ≠ 0 существует некоторое количество справедливых ставок, которые могут быть приняты.

* * *Разумеется, для значительного числа инвесторов, полагающих доход позитивным аспектом, а риск – негативным, и стремящихся избежать спекулятивных действий, правило «Е-V» применимо как в качестве рабочей гипотезы, так и в качестве рекомендации к действиям. Напрашиваются две основных области применения принципа «Е-V». Принцип может быть использован в теоретическом анализе поведения инвесторов или для выбора объекта реальных инвестиций на фондовом рынке.

В теоретическом анализе возможно, к примеру, изучение различных эффектов при изменении ожиданий, связанных с конкретной компанией или общих изменений предпочтений между ожидаемым доходом и дисперсией дохода, или изменений предложения ценной бумаги. При анализе в качестве X_i может выступать отдельная ценная бумага или композиты, включающие, например облигации, акции и доли в недвижимости. Результаты, полученные данным методом для композитов следует интерпретировать с осторожностью, однако здесь мы не углубляемся в обсуждение возникающих сложностей при переходе от индивидуальных бумаг к композитам.

При использовании правила «Е-V» для формирования портфеля необходимо выбрать алгоритм определения приемлемых исходных µ_i и σ_ij. Автор полагает, что такой метод будет сочетать статистический анализ исторических данных и экспертные суждения. Статистические расчеты могут использоваться для предварительного определения µ_i, и σ_ij. Затем, на основании экспертных суждений, могут быть сделаны корректировки значений исходя из факторов, которые не могут быть учтены в вычислениях на основе исторических данных. Имея на руках уточненные µ_i, и σ_ij, можно вычислить эффективные комбинации (E, V). После этого, инвестор сможет выбрать предпочтительную для него комбинацию, позволяющую подобрать эффективный портфель, имеющий характеристиками именно выбранные E и V.

В этом исследовании был рассмотрен второй этап процесса выбора портфеля. Второй этап опирается на установку разумных ожиданий о будущей доходности ценных бумаг и заканчивается выбором портфеля. Первый этап, заключающийся в анализе исторических данных и формировании ожиданий относительно будущей доходности доступных для инвестирования ценных бумаг, в данном исследовании не рассматривался.

 

---

---

---

Комментариев: 4 »