Риск и стандартное отклонение

Майкл Эдлесон
Из книги
«Усреднение ценности. Простая и надежная стратегия повышения доходности инвестиций на фондовом рынке»
Врезка к Главе 1 «Рыночный риск, тайминг и формульные стратегии»

Всякий раз, когда результат (например, доходность на рынке акций в следующем году) является случайным, он может принимать множество вероятных значений. Эти исходы (возможные результаты) имеют некоторое среднее, или центральное, ожидаемое значение, вокруг которого они будут концентрироваться. Предположим, что среднее значение составляет 15%; это означает, что возможные результаты, хотя и будут носить случайный характер, сосредоточатся вокруг значения 15%. Было бы неплохо знать, насколько близко к среднему значению находится возможная доходность. Если разброс случайных доходностей лежит в широком диапазоне (скажем, от –50 до +60%), то можно сказать, что распределение случайных доходностей вокруг ожидаемого среднего значения содержит высокий риск. Это риск заключается в том, что фактический результат может находиться весьма далеко от ожидаемого значения, причем как в большую, так и в меньшую сторону. Менее рискованное распределение подразумевает, что выход фактических значений за пределы диапазона, например, 0–30% является маловероятным.

Один из методов измерения этого риска называется стандартным отклонением (standard deviation, St.D). В общем случае оно показывает типичное отклонение случайной величины от ее ожидаемого значения (центра). Расстояние до среднего значения в одно стандартное отклонение не является чем-то особенным; расстояние в два стандартных отклонения – уже необычно; если же фактическое значение отстоит на три стандартных отклонения — можно говорить о некоем редком явлении. Более строгий подход определяет стандартное отклонение как корень квадратный из дисперсии, где дисперсия – это среднеквадратическое расстояние от ожидаемого значения. Функция @std в большинстве пакетов электронных таблиц вычислит для вас стандартное отклонение любого диапазона. Выражается стандартное отклонение, как и среднее значение доходности акций, в процентах.

На рис. 1.9 представлено схематическое изображение стандартного нормального распределения, показывающее вероятность случайного исхода относительно его ожидаемого значения. Случайные результаты представлены по горизонтальной оси с точки зрения того, как далеко (на сколько стандартных отклонений) они отстоят от ожидаемого значения (центра). Обратите внимание, что наиболее вероятные случайные результаты расположены вблизи ожидаемого значения, а чем дальше они отстоят от него, тем ниже вероятность их появления. Вероятность того, что результат попадет в конкретный диапазон, определяется размером площади его сегмента, расположенного ниже кривой нормального распределения.

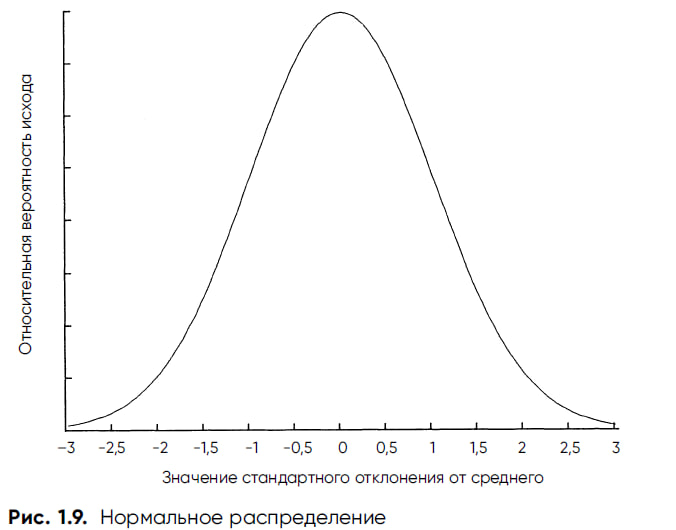
Например, существует вероятность 38,3%, что случайное значение выпадет между –0,5 и +0,5 стандартного отклонения от центра. Другие вероятности попадания на определенное расстояние от ожидаемого значения составляют:

• 68,3% — в пределах 1 St.D;
• 86,6% — в пределах 1,5 St.D;
• 95,4% — в пределах 2 St.D;
• 98,8% — в пределах 2,5 St.D.

Лишь четверть процента случайных величин окажется далее чем в трех стандартных отклонениях от центра.

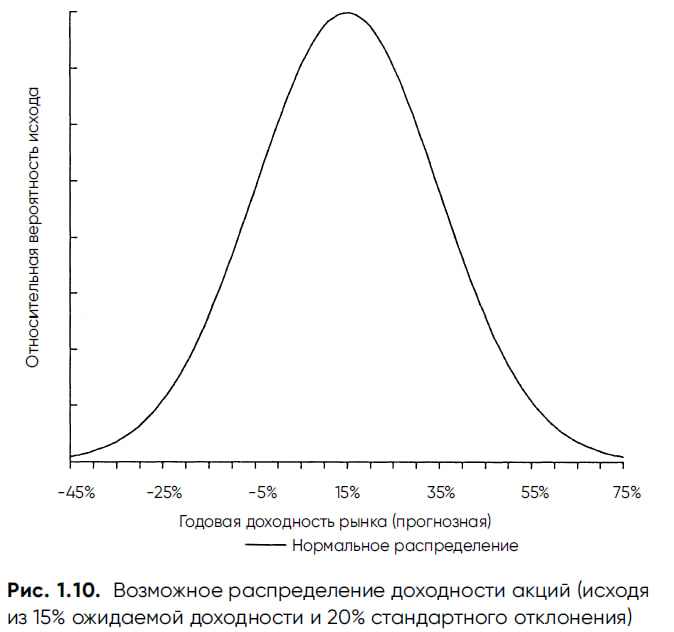
Таким образом, стандартное отклонение является мерой разброса случайных значений, которая позволяет нам «стандартизировать» их удаленность от центра. Это полезно для оценки вероятности различных доходностей акций. На рис. 1.10 показано одно из возможных случайных распределений доходностей рынка акций с использованием следующих значений: ожидаемая доходность – 15%, стандартное отклонение — 20%. Возможные годовые доходности отмечены на оси абсцисс с интервалом в одно стандартное отклонение (каждые 20% с центром, равным 15% доходности). Такая визуализация позволяет нам делать вероятностные оценки различных доходностей.

* * *

Расчет стандартного отклонения в Excel

(Примечание для российских читателей к врезке к врезке «Риск и стандартное отклонение»)

Для расчета стандартного отклонения в Excel используется формула:
=СТАНДОТКЛОНП (число1; [число2]; …).

Например, чтобы рассчитать стандартное отклонение доходностей индекса РТС за 2010–2019 гг. (10 лет), просто перечислите значения годовых доходностей за эти годы в скобках:

=СТАНДОТКЛОНП (24,6%; –20,4%; 14,5%; –1,6%; –42%; 0,4%; 59,4%; 5,8%; –1,8%; 56,1%).

Полученный ответ: 29,7%. Вместо перечня аргументов можно использовать ссылку на массив ячеек. Например, если расположить значения доходностей по годам в ячейках A1: A10, то формула =СТАНДОТКЛОНП (A1:A10) рассчитает стандартное отклонение доходностей в массиве.

Полезно знать, что в Excel есть формула для расчета вероятности попадания будущего результата в интересующий нас интервал доходности, если нам известны среднее значение доходностей («центр») и стандартное отклонение («размах»). Формула для расчета:

=НОРМРАСП (x; среднее; размах; интегральная),

где х — вероятность, ниже которой мы хотим оценить; «среднее» и «размах» – значения среднего арифметического и стандартного отклонения соответственно, а «интегральная» – поле для расчета вероятности, которое должно иметь значение «TRUE» или «1».

Например, если мы примем 15% в качестве «центра» (математического ожидания) и 20% в качестве «размаха» (стандартного отклонения), то формула для расчета вероятности попадания в интервал от –5 до +35% (плюс-минус одно стандартное отклонение) будет выглядеть следующим образом:

=НОРМРАСП (35%; 15%; 20%; 1) —НОРМРАСП (–5%; 15%; 20%; 1).
Ответ: 68%.

---

---

---

Комментариев нет »